【题目】计算:
(1)![]() ;
;
(2)![]()
(3)![]() (代入消元法);
(代入消元法);
(4)![]() (加减消元法)
(加减消元法)
解不等式组,并把解集在数轴上表示出来:
(5)![]() ;
;
(6)
参考答案:
【答案】(1)2-![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() ,(4)
,(4)![]() ;(5)-1<x<2,见解析;(6)x>3,见解析.
;(5)-1<x<2,见解析;(6)x>3,见解析.
【解析】
(1)根据二次根式的性质,绝对值的性质,立方根的定义,进行化简求值即可;
(2)化简绝对值,然后合并同类二次根式即可;
(3)由代入消元法,即可解出方程组的解;
(4)由加减消元法,即可解出方程组的解;
(5)分别求出两个不等式的解集,得到不等式组解集,然后表示在数轴上即可;
(6)分别求出两个不等式的解集,得到不等式组解集,然后表示在数轴上即可.
解:(1)原式=![]() ;
;
(2)原式=![]() ;
;
(3)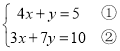
由①得,y=5-4x ③,
把③代入②,得3x+7(5-4x)=10,
解得:x=1,
把x=1代入③,得y=1,
所以方程组的解为![]() ;
;
(4)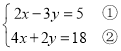 ,
,
①×2+②×3,得16x=64,x=4,
把x=4代入①,得8-3y=5,y=1,
所以方程组的解是![]() ;
;
(5)![]() ,
,
解不等式2x+3>1,得:![]() ,
,
解不等式x-2<0,得:x<2,
则不等式组的解集为:![]() ,
,
将解集表示在数轴上如下:

(6)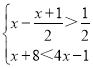
解不等式x-![]() >
>![]() ,得:x>2,
,得:x>2,
解不等式x+8<4x-1,得:x>3,
则不等式组的解集为x>3,
将不等式组的解集表示在数轴上如下:
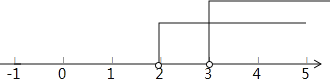 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BC=6cm,点E从点D出发沿DA边运动到点A,点F从点B出发沿BC边向点C运动,点E的运动速度为2cm/s,点F的运动速度为lcm/s,它们同时出发,设运动的时间为t秒,当t为何值时,EF∥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且AF=FC,GH⊥CD于H.下列说法①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH∶∠ECH=2∶7,则∠EGH=40°.其中正确的有________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为6×6的正方形网格,每个小正方形的顶点均为格点,在图中已标出线段AB,A,B均为格点,按要求完成下列问题.
(1)以AB为对角线画一个面积最小的菱形AEBF,且E,F为格点;
(2)在(1)中该菱形的边长是 ,面积是 ;
(3)以AB为对角线画一个菱形AEBF,且E,F为格点,则可画 个菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=
 的图像经过B、C两点.
的图像经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图像探索:当y>0时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
相关试题

