【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
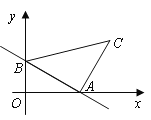
轴、![]() 轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
参考答案:
【答案】解:一次函数![]() 中,令
中,令![]() 得:
得:![]() ;令
;令![]() ,解得
,解得![]() 。
。
∴A的坐标是(0,2),C的坐标是(3,0).
作CD⊥![]() 轴于点D。
轴于点D。

∵∠BAC=90°,∴∠OAB+∠CAD=90°。
又∵∠CAD+∠ACD=90°,∴∠ACD=∠BAO。
又∵AB=AC,∠BOA=∠CDA=90°,∴△ABO≌△CAD(AAS)。
∴AD=OB=2,CD=OA=3,OD=OA+AD=5。∴C的坐标是(5,3)。
设BC的解析式是![]() ,
,
根据题意得:![]() ,解得:
,解得:![]() 。
。
∴BC的解析式是:![]() 。
。
【解析】一次函数综合题,全等三角形的判定和性质,待定系数法,直线上点的坐标与方程的关系。
-
科目: 来源: 题型:
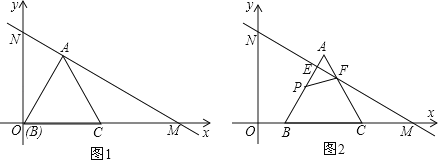
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6cm,∠OMN=30°,等边△ABC的顶点B与原点O重合,BC边落在x轴的正半轴上,点A恰好落在线段MN上,如图2,将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移,边AB、AC分别与线段MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s),△PEF的面积为S(cm2).
(1)求等边△ABC的边长;
(2)当点P在线段BA上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线B→A→C运动的过程中,是否在某一时刻,使△PEF为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,不正确的是( )
A.零是整数
B.零没有倒数
C.零是最小的数
D.-1是最大的负整数 -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列关于x的不等式(组):
(1)
 (2)
(2)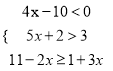
(3)
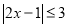 (4)
(4) 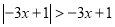
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.
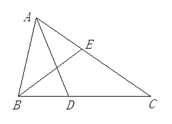
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织初一、初二学生举行“四城同创”宣传活动,从学校坐车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度保持不变,在A地仍要宣传8分钟,则他们从B地返回学校用的时间是( )
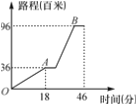
A. 48分钟 B. 45.2分钟 C. 46分钟 D. 33分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不相等的一组是( )
A.-(+7), -|-7|
B.-(+7),-|+7|
C.+(-7), -(+7)
D.+(+7), -|-7|
相关试题

