【题目】已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为-5,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.
秒.
(1)BP= ,点P表示的数 (分别用含![]() 的代数式表示);
的代数式表示);
(2)点P运动多少秒时,PB=2PA?
(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)3秒或9秒;(3)长度不发生变化,长度是9.
;(2)3秒或9秒;(3)长度不发生变化,长度是9.
【解析】试题分析:(1)根据BP=速度×时间可表示出BP的长,点P表示的数为-5+4t;
(2) 分点P在AB之间运动时和点P在运动到点A的右侧时两种情况列出方程求解即可;
(3) 分点P在AB之间运动时和点P在运动到点A的右侧时两种情况,利用中点的定义和线段的和差求出MN的长即可.
解:(1)由题意得,BP=4t,点P表示的数是-5+4t;
(2)当点P在AB之间运动时,由题意得,
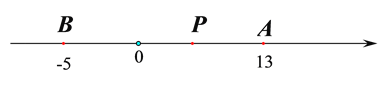
PB=4t,PA=13-(-5+4t)=18-4 t,
∵PB=2PA,
∴4t=2(18-4 t),
∴t=3;
当点P在运动到点A的右侧时,由题意得,

PB=4t,PA=-5+4t-13=4 t -18,
∵PB=2PA,
∴4t=2(4 t -18),
∴t=9;
综上可知,点P运动多3秒或9秒时,PB=2PA.
(3)当点P在AB之间运动时,由题意得,

PB=4t,PA=18-4 t,
∵M为BP的中点,N为PA的中点,
∴![]() ,
,![]() ,
,
∴MN=MP+NP=2t+9-2t=9;
当点P在运动到点A的右侧时,由题意得,

PB=4t,PA=4 t -18,
∵M为BP的中点,N为PA的中点,
∴![]() ,
,![]() ,
,
∴MN=MP-NP=2t-(2t-9)=9;
综上可知,线段MN的长度不发生变化,长度是9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A所表示的实数为5,点B所表示的实数为a,⊙A的半径为3,要使点B在⊙A内时,实数a的取值范围是( )
A.a>2B.a>8C.2<a<8D.a<2或a>8
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于2且不大于5的整数有_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤
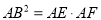 .其中正确的个数为( ).
.其中正确的个数为( ). 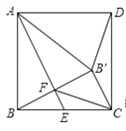
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式2x﹣x2﹣1+x3按x的降幂排列是_____.
相关试题

