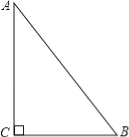
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为12?
参考答案:
【答案】(1)6 (2)6.5 (3)2或6.5
【解析】试题分析:(1)由△ABC的周长为24时,当CP把△ABC的周长分成相等的两部分时,点C所以过的路程为12cm,再求时间即可;(2)由![]() 的面积等于
的面积等于![]() 的一半;设
的一半;设![]() 为
为![]() 的高,则
的高,则![]() ,则
,则![]() ,所以点
,所以点![]() 应为
应为![]() 的中点,所以点运动的路程为
的中点,所以点运动的路程为![]() ,再求时间即可;(3)分两种情况讨论,当点P在AC上时,由
,再求时间即可;(3)分两种情况讨论,当点P在AC上时,由![]() ×6×CP=12,得出CP=4,此时运动时间为2秒;当当P在AB上时,P运动到AB的中点,运动路程为13cm,求时间即可;
×6×CP=12,得出CP=4,此时运动时间为2秒;当当P在AB上时,P运动到AB的中点,运动路程为13cm,求时间即可;
试题解析:
(1)△ABC中,∵AC=8cm,BC=6cm,AB=10cm,∴△ABC的周长=8+6+10=24cm,∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,∴2t=12,t=6;(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),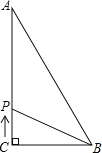
∴2t=13,t=6.5;
(3)分两种情况:①当P在AC上时,∵△BCP的面积=12,即![]() ×6×CP=12,∴CP=4,∴2t=4,t=2;②当P在AB上时,∵△BCP的面积=12=△ABC面积的一半,∴P为AB中点,∴2t=13,t=6.5.故答案为6秒;6.5秒.
×6×CP=12,∴CP=4,∴2t=4,t=2;②当P在AB上时,∵△BCP的面积=12=△ABC面积的一半,∴P为AB中点,∴2t=13,t=6.5.故答案为6秒;6.5秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正五边形的外角和等于 (度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴正半轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线OA'交于点F.
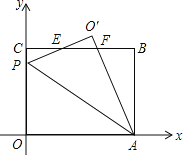
(1)当点P在y轴正半轴,且∠OAP=30°时,求点O′的坐标;
(2)当O′落在直线BC上时,求直线O′A的解析式;
(3)当点P在矩形OABC边OC的运动过程中,是否存在某一时刻,使得线段CF与线段OP的长度相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C;②∠A﹕∠B﹕∠C=1﹕2﹕3;③∠A=
 ∠B=
∠B= ∠C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠C;④∠A=∠B=2∠C;⑤∠A=∠B= ∠C,能确定△ABC为直角三角形的条件有( )
∠C,能确定△ABC为直角三角形的条件有( )A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
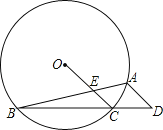
(1)求∠D的度数;
(2)若CE=3,AD=4,求线段AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(3,5)关于x轴的对称点的坐标为
A. (3,-5) B. (-3,-5) C. (-3,5) D. (-5,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:27x2+18x+3= . 2x2﹣8= .
相关试题

