搜索
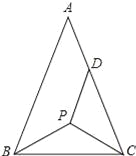
【题目】如图，等腰△ABC中，AB=AC，P为其底角平分线的交点，将△BCP沿CP折叠，使B点恰好落在AC边上的点D处，若DA=DP，则∠A的度数为__．
参考答案：
【答案】36°
【解析】解：连接AP．∵P为其底角平分线的交点，∴点P是△ABC的内心，∴AP平分∠BAC，∵AB=AC，∴∠ABC=∠ACB，设∠A=2x，则∠DAP=x，∠PBC=∠PCB=45°﹣
x，∵DA=DP，∴∠DAP=∠DPA，由折叠的性质可得：∠PDC=∠PBC=45°﹣
x，则∠ADP=180°﹣∠PDC=135°+
x，在△ADP中，∠DAP+∠DPA+∠ADP=180°，即x+x+135°+
x=180°，解得：x=18，则∠A=2x=36°．故答案为：36°．
-
科目： 来源： 题型：
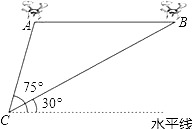
查看答案和解析>>【题目】某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】本学期实验中学组织开展课外兴趣活动，各活动小班根据实际情况确定了计划组班人数，并发动学生自愿报名，报名人数与计划人数的前5位情况如下．若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度，则由表中数据，可预测（ ）
小班名称
奥数
写作
舞蹈
篮球
航模
报名人数
215
201
154
76
65
小班名称
奥数
舞蹈
写作
合唱
书法
计划人数
120
100
90
80
70
A.奥数比书法容易
B.合唱比篮球容易
C.写作比舞蹈容易
D.航模比书法容易 -
科目： 来源： 题型：
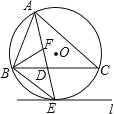
查看答案和解析>>【题目】如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．
（1）判断直线l与⊙O的位置关系，并说明理由；
（2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；
（3）在（2）的条件下，若DE=4，DF=3，求AF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数y＝2（x﹣1）2﹣8，下列说法正确的是（ ）
A.图象开口向下
B.当x＞1时，y随x的增大而减小
C.当x＜1时，y随x的增大而减小
D.图象的对称轴是直线x＝﹣1
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a2－2a－1＝0，则2a2－4a＋5＝________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
（1）求y与x之间的函数关系式；
（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？
相关试题
