【题目】如图,已知A(﹣2,4),B(4,2),C(2,﹣1)
(1)作△ABC关于x轴的对称图形△A1B1C1,写出点C关于x轴的对称点C1的坐标;
(2)P为x轴上一点,请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标(保留作图痕迹).
参考答案:
【答案】详见解析.
【解析】试题分析:
(1) 先根据题目给出的已知点的坐标,在图中的相应位置上标出原三角形的三个顶点. 根据关于x轴对称的点的坐标规律,将对称变换后的三角形的顶点坐标写出,即A1 (-2, -4),B1 (4, -2),C1 (2, 1). 在图中相应的位置上标出对称变换后的三角形的三个顶点. 连接这三个顶点即得所求的△A1B1C1. 至于题目中有关写出点C1坐标的问题,可以根据前面得到的点C1的坐标作答即可.
(2) △PAB的周长为PA+PB+AB. 由于点A和点B均为坐标已知的固定点,所以线段AB的长度是一个定值. 因此,△PAB的周长最小就是PA+PB最小. 这种最小值问题可以利用轴对称进行求解. 先将点A关于x轴的对称点A1画出:过点A作x轴的垂线(为叙述方便,设垂足为点D),在线段AD的延长线上截取DA1=DA,则点A1即为点A关于x轴的对称点. 然后,连接A1B,交x轴于点P,则点P即为所求. 观察图形不难看出,点P的坐标为(2, 0).
试题解析:
(1) 如图所示,△A1B1C1即为所求.
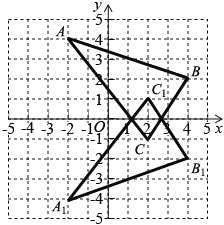
∵点C与点C1关于x轴对称,
又∵点C的坐标为(2, -1),
∴点C1的坐标为(2, 1).
(2) 如图所示,点P即为所求.
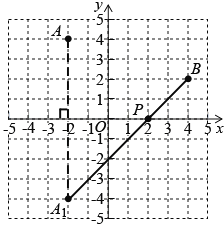
根据上述图形可知,点P的坐标为(2, 0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有 ①体育场离小冬家2.5千米 ②小冬在体育场锻炼了15分钟
③体育场离早餐店4千米 ④小冬从早餐店回家的平均速度是3千米/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果3y9﹣2m+2=0是关于y的一元一次方程,则m=
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3x2y+5xy=8x3y2B.(x+y)2=x+yC.(-2x)2÷x=4xD.a6÷a3=a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.
(1)求这个抛物线的表达式;
(2)求点P的坐标;
(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对该校九年级45名女学生进行了一次立定跳远测试,成绩如表:
跳远成绩
160
170
180
190
200
210
人数
3
9
6
9
15
3
这些立定跳远成绩的中位数和众数分别是( )
A.9,9B.15,9C.190,200D.185,200
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(),
∴∠2=∠CGD(等量代换).
∴CE∥BF().
∴∠=∠C().
又∵∠B=∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD().
相关试题

