【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1 , x2 , 且x1![]() x2有下列结论:
x2有下列结论:
①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).
其中正确的结论是(填正确结论的序号)
参考答案:
【答案】②、③
【解析】首先将这个方程转化成一般形式,然后根据根的判别式可以判定m的取值范围;如果m=0,则方程的解为2或3,但是本题没有说明m=0,则方程的解不一定为2或3.
【考点精析】掌握求根公式和抛物线与坐标轴的交点是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
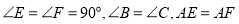 ,结论:①
,结论:①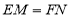 ;②
;②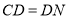 ;③
;③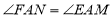 ;④
;④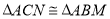 ,其中正确的是有( )
,其中正确的是有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在△ABC,∠BAC=135°,AB⊥AD,DC=AB+AD,则∠ACB=______度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
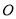 为△
为△ 中
中 与
与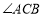 的平分线的交点,分别过点
的平分线的交点,分别过点 、
、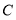 作
作 ,
,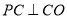 ,若
,若 °,你能够求出
°,你能够求出 的度数吗?若能请写出解答过程.
的度数吗?若能请写出解答过程.
-
科目: 来源: 题型:
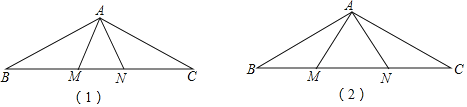
查看答案和解析>>【题目】已知如图,M、N是△ABC的BC边上两点,且AB=AC,BM=CN
(1)如图1,证明:△ABN≌△ACM;
(2)如图2,当∠ANB=2∠B时,直接写出图中所有等腰三角形(△ABC除外)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=
 ∠BAD.求证:EF=BE+FD.
∠BAD.求证:EF=BE+FD. 
相关试题

