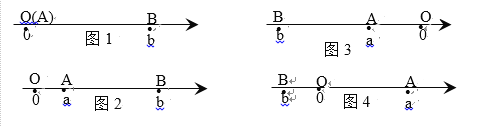
【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;
如图3,点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;
如图4,点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列问题:
(1)数轴上表示3和7的两点之间的距离是 ,数轴上表示-1和-3的两点之间的距离是 ,数轴上表示1和-2的两点之间的距离是 .
(2)数轴上表示x和-2的两点A和B之间的距离是 ,如果∣AB∣=2,那么x为 ;
(3)当代数式∣x∣+∣x-1∣取最小值时,最小值是 .
参考答案:
【答案】(1)4、2、3;(2)![]() 、0或-4(3)1
、0或-4(3)1
【解析】(1)4、2、3;
(2)数轴上表示x和-2的两点A和B之间的距离是![]() 如果∣AB∣=2,则x+2=2或-2
如果∣AB∣=2,则x+2=2或-2
得出x=0或-4
(3)当x在0和1之间时,∣x∣+∣x-1∣取最小值时1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:3a2﹣27=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
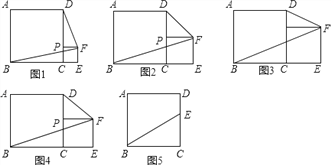
观察计算:(1)如图1,当a=4,b=1时,四边形ABFD的面积为 ;
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 ;
探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?
综合应用:
(5)农民赵大伯有一块正方形的土地(如图5),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你在图5中画图确定M点的位置.并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1:已知△ABC中,∠BAC=90°,AB=AC,在∠BAC内部作∠MAN=45°.AM、AN分别交BC于点M,N.
(1)将△ABM绕点A逆时针旋转90°,使AB边与AC边重合,把旋转后点M的对应点记作点Q,得到ACQ,请在图1中画出△ACQ;(不写出画法)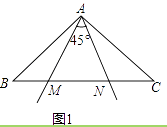
(2)在(1)中作图的基础上,连接NQ,
①求证“MN=NQ”;
②写出线段BM,MN和NC之间满足的数量关系,并简要说明理由.
(3)线段GS,ST和TH之间满足的数量关系是
(4)设DK=a,DE=b,求DP的值.(用a,b表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
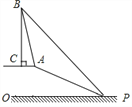
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的立方体的六个面分别标着连续的整数,求这六个整数的和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】气魄雄伟的大礼堂座落在渝中区学田湾,它是一座仿古民族建筑.“五一”期间,小明和妈妈到重庆大礼堂参观游玩.参观结束后,穿过人民广场到达A处,回望礼堂,更显气势雄伟,金碧辉煌.此时,在A点观察到礼堂顶端的仰角为30°,沿着坡度为1:3的斜坡AB走一段距离到达B点,观察到礼堂顶端 的仰角是22°,测得点A与BC之间的水平距离
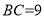 米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:
米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:  ,
, 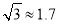 .)
.)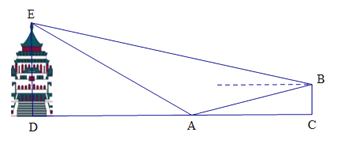
A. 58 B. 60 C. 62 D. 64
相关试题

