【题目】如图，正方形ABCD的边长为1，E是AD边上一动点，AE=m，将△ABE沿BE折叠后得到△GBE．延长BG交直线CD于点F．

（1）若∠ABE：∠BFC=n，则n= ______ ；

（2）当E运动到AD中点时，求线段GF的长；

（3）若限定F仅在线段CD上（含端点）运动，求m的取值范围．

参考答案：

【答案】（1） 2；（2）线段GF的长为；（3）m的取值范围是： -1≤m≤1．

【解析】试题分析： 根据正方形的性质可得，根据折叠可得，由此得出的值即可；
先根据折叠的性质，判定，再设，在 中运用勾股定理求得的值即可；
若限定仅在线段上（含端点）运动，则分两种情况进行讨论：点与点重合，点与点重合，进而求得的取值范围．

试题解析： 正方形中, ,

由折叠得，

故答案为：

当运动到中点时，

由折叠得,

根据 可得,

设，则

∵在中,

解得:

∴线段的长为

（3）若限定仅在线段上（含端点）运动，则

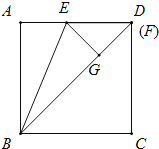
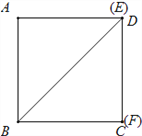
①如图，当点与点重合时，

在中，

解得（舍去），

②如图，当点与点重合时，点与点重合，此时

综上， 的取值范围是：

关闭