搜索
【题目】如图是同一时刻学校里一棵树和旗杆的影子，如果树高为3米，测得它的影子长为1.2米，旗杆的高度为5米，则它的影子长为（ ） 
A.4米
B.2米
C.1.8米
D.3.6米
参考答案：
【答案】B
【解析】解：设旗杆的影长为x米，
根据在同一时刻同一地点任何物体的高与其影子长的比值相同得： 
，
解得：x=2．
故选：B．
【考点精析】根据题目的已知条件，利用相似三角形的应用和平行投影的相关知识可以得到问题的答案，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解；太阳光线可以看成是平行光线，平行光线所形成的投影称为平行投影；作物体的平行投影：由于平行投影的光线是平行的，而物体的顶端与影子的顶端确定的直线就是光线，故根据另一物体的顶端可作出其影子．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图某商场为了吸引顾客,设立了一个可以自由转动的转盘，并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、20、100、50、10的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张。(转盘等分成20份)
(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么她获得100元以上(包括100元)券的概率是多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.5厘米,每个铁环长4.6厘米,设铁环间处于最大限度的拉伸状态
(1)填表:
铁环个数
1
2
3
4
链条长(cm)
4.6
8.2
_____
____
(2)设n个铁环长为y厘米,请用含n的式子表示y；
(3)若要组成2.17米长的链条,至少需要多少个铁环?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线y=ax2+bx+3（a≠0）与x轴、y轴分别交于点A（﹣1，0）、B（3，0）、点C三点．
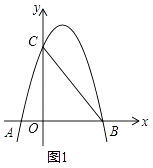
（1）试求抛物线的解析式；
（2）点D（2，m）在第一象限的抛物线上，连接BC，BD．试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由；
（3）如图2，在（2）的条件下，将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，记平移后的三角形为△B′O′C′．在平移过程中，△B′O′C′与△BCD重叠的面积记为S，设平移的时间为t秒，试求S与t之间的函数关系式？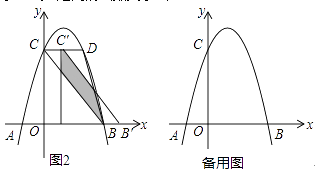
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列哪组条件能够判别四边形ABCD是平行四边形？（ ）
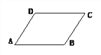
A. AB∥CD，AD＝BC B. AB＝CD，AD＝BC
C. ∠A＝∠B，∠C＝∠D D. AB＝AD，CB＝CD
-
科目： 来源： 题型：
查看答案和解析>>【题目】（题文）直角三角形有一个非常重要的性质质:直角三角形斜边上的中线等于斜边的一半,比如:如图1,Rt△ABC中,∠C=90°,D为斜边AB中点,则CD=AD=BD=-AB.请你利用该定理和以前学过的知识解决下列问题:
在△ABC中,直线
绕顶点A旋转.(1)如图2,若点P为BC边的中点,点B、P在直线
的异侧,BM⊥直线于点M,CN⊥直线于点N,连接PM、PN.求证:PM=PN；(2)如图3,若点B、P在直线
的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明；若不成立,请说明理由；(3)如图4,∠BAC=90°,直线
旋转到与BC垂直的位置,E为AB上一点且AE=AC，EN⊥于N,连接EC,取EC中点P,连接PM、PN,求证:PM⊥PN.
相关试题
