Question

【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线OD交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC度数为( ).

A. 108° B. 135° C. 144° D. 160°

Answer 1

【答案】A

【解析】

连接OB、OC，根据角平分线的定义求出∠BAO，根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB，根据等边对等角可得∠ABO=∠BAO，再求出∠OBC，然后判断出点O是△ABC的外心，根据三角形外心的性质可得OB=OC，再根据等边对等角求出∠OCB=∠OBC，根据翻折的性质可得OE=CE，然后根据等边对等角求出∠COE，再利用三角形的内角和定理列式计算即可得解．

解：如图，连接OB、OC，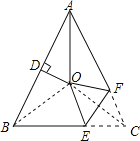

∵∠BAC=54°，AO为∠BAC的平分线，
∴∠BAO=∠BAC=×54°=27°，
又∵AB=AC，
∴∠ABC=（180°-∠BAC）=（180°-54°）=63°，
∵DO是AB的垂直平分线，
∴OA=OB，
∴∠ABO=∠BAO=27°，
∴∠OBC=∠ABC-∠ABO=63°-27°=36°，
∵AO为∠BAC的平分线，AB=AC，
∴△AOB≌△AOC（SAS），
∴OB=OC，
∴点O在BC的垂直平分线上，
又∵DO是AB的垂直平分线，
∴点O是△ABC的外心，
∴∠OCB=∠OBC=36°，
∵将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，
∴OE=CE，
∴∠COE=∠OCB=36°，
在△OCE中，∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°．
故选：A．