【题目】2013年4月20日,四川雅安发生7.0级地震,给雅安人民的生命财产带来巨大损失.某市民政部门将租用甲、乙两种货车共16辆,把粮食266吨、副食品169吨全部运到灾区.已知一辆甲种货车同时可装粮食18吨、副食品10吨;一辆乙种货车同时可装粮食16吨、副食11吨.
(1)若将这批货物一次性运到灾区,有哪几种租车方案?
(2)若甲种货车每辆需付燃油费1500元;乙种货车每辆需付燃油费1200元,应选(1)中的哪种方案,才能使所付的费用最少?最少费用是多少元?
参考答案:
【答案】
(1)解:设租用甲种货车x辆,租用乙种货车为(16﹣x)辆,
根据题意得, ![]() ,
,
由①得,x≥5,
由②得,x≤7,
∴,5≤x≤7,
∵x为正整数,
∴x=5或6或7,
因此,有3种租车方案:
方案一:租甲种货车5辆,乙种货车11辆;
方案二:租甲种货车6辆,乙种货车10辆;
方案三:租甲种货车7辆,乙种货车9辆
(2)解:方法一:由(1)知,租用甲种货车x辆,租用乙种货车为(16﹣x)辆,设两种货车燃油总费用为y元,
由题意得,y=1500x+1200(16﹣x),
=300x+19200,
∵300>0,
∴y随x值增大而增大,当x=5时,y有最小值,
∴y最小=300×5+19200=20700元;
方法二:
当x=5时,16﹣5=11,
5×1500+11×1200=20700元;
当x=6时,16﹣6=10,
6×1500+10×1200=21000元;
当x=7时,16﹣7=9,
7×1500+9×1200=21300元;
答:选择(1)中的方案一租车,才能使所付的费用最少,最少费用是20700元
【解析】(1)设租用甲种货车x辆,表示出租用乙种货车为(16﹣x)辆,然后根据装运的粮食和副食品数不少于所需要运送的吨数列出一元一次不等式组,求解后再根据x是正整数设计租车方案;(2)方法一:根据所付的费用等于两种车辆的燃油费之和列式整理,再根据一次函数的增减性求出费用的最小值; 方法二:分别求出三种方案的燃油费用,比较即可得解.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中, B(0,8),D(10,0),一次函数y=
 x+
x+ 的图象过C(16,n),与x轴交于A点。
的图象过C(16,n),与x轴交于A点。(1)求证:四边形ABCD为平行四边形;
(2)将△AOB绕点O顺时针旋转,旋转得△A1OB1,问:能否使以点O、A1、D、B1为顶点的四边形是平行四边形?若能,求点A1的坐标;若不能,请说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,如果直线l上依次有3个点A、B、C,那么

(1)在直线l上共有多少射线?多少条线段?
(2)在直线l上增加一个点,共增加了多少条射线?多少条线段?
(3)如果在直线l上增加到n个点,则共有多少条射线?多少条线段?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过对角线BD上一点P,作EF∥BC,HG∥AB,若四边形AEPH和四边形CFPG的面积分另为S1和S2,则S1与S2的大小关系为( )
A.S1=S2 B.S1>S2 C.S1<S2 D.不能确定

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
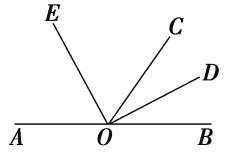
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( )

A.甲<乙<丙 B.乙<丙<甲
C.丙<乙<甲 D.甲=乙=丙
-
科目: 来源: 题型:
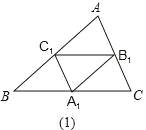
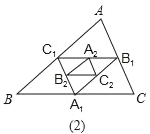
查看答案和解析>>【题目】如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB上的点,且A1C1∥AC,A1B1∥AB,B1C1∥BC,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1上的点,且A2C2∥A1C1,A2B2∥A1B1,B2C2∥B1C1,…,按此规律,则第n个图形中平行四边形的个数共有__个.

相关试题

