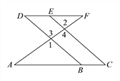
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )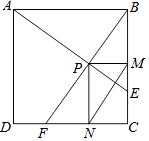
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】D
【解析】解:如图,
∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中,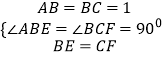
∴△ABE≌△BCF(SAS),故①正确;
∴∠BAE=∠CBF,AE=BF,故②正确;
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,故③正确;
在△BPE和△BCF中,
∵∠BPE=∠BCF,∠PBE=∠CBF,
∴△BPE∽△BCF,
∴ ![]() =
= ![]() ,
,
∴CFBE=PEBF,
∵CF=BE,
∴CF2=PEBF,故④正确;
∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG= ![]() =
= ![]() =
= ![]() ,
,
∵PG= ![]() AB=
AB= ![]() ,
,
∴CP=CG﹣PG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
即线段CP的最小值为 ![]() ,故⑤正确;
,故⑤正确;
综上可知正确的有5个,
故选D.
由正方形的性质及条件可判断出①△ABE≌△BCF,即可判断出②AE=BF,∠BAE=∠CBF,再根据∠BAE+∠BEA=90°,可得∠CBF+∠BEA=90°,可得出∠APB=90°,即可判断③,由△BPE∽△BCF,利用相似三角形的性质,结合CF=BE可判断④;然后根据点P在运动中保持∠APB=90°,可得点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△BCG中,根据勾股定理,求出CG的长度,再求出PG的长度,即可求出线段CP的最小值,可判断⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.

(1)几秒后P,Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,
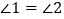 ,
,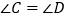 ,求证:DF∥AC.
,求证:DF∥AC.证明:∵
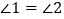 (已知),∠1=∠3,∠2=∠4( ),
(已知),∠1=∠3,∠2=∠4( ),∴∠3=∠4(等量代换).
∴__________
 __________( ).
__________( ).∴∠C=∠ABD( ).
∵∠C=∠D( ),
∴∠D=__________( ).
∴AC∥DF( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据你的经验,分别求下列事件的概率:
(1)在一个不透明的袋中装有红球3个,白球2个,黑球1个,每种球除颜色外其余都相同,摇匀后随机地从袋中取出1个球,取到红球的概率.
(2)投掷一枚普通正方体骰子,出现的点数为7的概率.
(3)投掷两枚普通硬币,出现两个正面的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为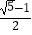 .
.
其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

-
科目: 来源: 题型:
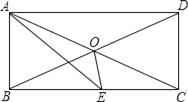
查看答案和解析>>【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
相关试题

