【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
参考答案:
【答案】甲;![]() ≠1-a.
≠1-a.
【解析】
首先对根号里的数或代数式通过完全平方公式、平方差公式等进行化简,注意在去掉根号时,要对化简后的结果带上绝对值,再根据已知参数的值看看绝对值里的代数式与零的大小关系,最后去掉绝对值即可得到最简结果,再将参数的值代入即可.
解:甲是错误的,,没有根据a的取值正确的去掉绝对值符号.
理由:a+![]() ,由完全平方式,得a+
,由完全平方式,得a+![]() ,化简,得a+|1a|,
,化简,得a+|1a|,
当a=9时,1-a<0,故对a+|1a|去掉绝对值符号,得a-1+a,
合并同类项,得:2a-1,
将a=9代入2a-1,得2×9-1=17
所以甲的答案错误,错误的原因是没有根据a的取值正确的去掉绝对值符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D,E分别在边BC 和AC上,若AD=AE,则下列结论错误的是( )
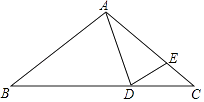
A.∠ADB=∠ACB+∠CAD
B.∠ADE=∠AED
C.∠CDE= ∠BAD
∠BAD
D.∠AED=2∠ECD -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F.
(1)求CE的长;
(2)建立平面直角坐标系如图②所示,在x轴上找一点P,使PA+PE的值最小,求出最小值和点P的坐标;
(3)如图③,DE的延长线与AF的延长线交于点G,在y轴上是否存在点M,使△FGM是直角三角形?如果存在,求出点M的坐标:如果不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随即抽查部分同学体育测试成绩(由高到低分四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图:
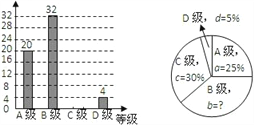
请根据以上不完整的统计图提供的信息,解答下列问题:
(1) 该课题研究小组共抽查了_________名同学的体育测试成绩,扇形统计图中B级所占的百分比b=__________
(2) 补全条形统计图.
(3) 若该校九年级共有200名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)均有___________名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:
已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
小明发现,可以设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴
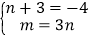
利用方程组可以解决.
请回答:
另一个因式为 ,m的值为 ;
参考小明的方法,解决下面的问题:
已知二次三项式2x2+3x﹣k有一个因式是(x﹣4),求另一个因式以及k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.
请根据以上信息回答: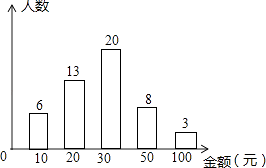
(1)该班同学所抢红包金额的众数是 , 中位数是;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(﹣6,7),(﹣3,0),(0,3).
(1)画出三角形ABC,并求三角形ABC的面积;
(2)将三角形ABC平移得到三角形A′B′C′,点C经过平移后的对应点为C′(5,4),画出平移后的三角形A′B′C′,并写出点A′,B′的坐标:A′(________),B′(________)
(3)已知点P(﹣3,m)为三角形ABC内一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,﹣3),则m=________,n=________.

相关试题

