【题目】如图,抛物线![]() 交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒
交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.

参考答案:
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)当t1=
;(3)当t1=![]() 秒,此时路径长度为
秒,此时路径长度为![]() ,当t2=5秒,此时路径长度为
,当t2=5秒,此时路径长度为![]() .
.
【解析】试题分析:(1)利用待定系数法求二次函数的解析式;
(2)先表示G的坐标,再把点G的坐标代入抛物线的解析式中列方程可得t的值;
(3)如图2,先计算当G在BD上时,t的值;
分三种情况进行讨论:
①当0≤t≤![]() 时,如图3,作辅助线,根据S△BCG=S梯形GHDB+S△BDC﹣S△GHC,列式可得t的值,利用勾股定理求AG的长即可;
时,如图3,作辅助线,根据S△BCG=S梯形GHDB+S△BDC﹣S△GHC,列式可得t的值,利用勾股定理求AG的长即可;
②当G在BC上时,如图4,根据同角的三角函数得tan∠C=![]() =2,则GH=2HC,列关于t的方程得:t=
=2,则GH=2HC,列关于t的方程得:t=![]() ;当
;当![]() <t≤
<t≤![]() 时,如图5,同理可得结论;
时,如图5,同理可得结论;
③当E与D重合时,F与B重合,如图6,此时t=4,计算此时△BCG的面积为2,因此点G继续向前运动;
当t>4时,如图7,同理列方程可得结论.
试题解析:解:(1)将B(4,4)和C(6,0)代入抛物线![]() 得:
得: ![]() ,解得:
,解得:  ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() ;
;
(2)如图1,由题意得:AE=![]() t,∵A(0,4),B(4,4),∴AB⊥y轴,且AB∥x轴,∵OA=OD=4,∴△AOD是等腰直角三角形,∴∠ADO=∠BAD=45°,∴△AFE是等腰直角三角形,∴AF=EF=t,∵△EFG是等腰直角三角形,∴G(t+
t,∵A(0,4),B(4,4),∴AB⊥y轴,且AB∥x轴,∵OA=OD=4,∴△AOD是等腰直角三角形,∴∠ADO=∠BAD=45°,∴△AFE是等腰直角三角形,∴AF=EF=t,∵△EFG是等腰直角三角形,∴G(t+![]() t,4﹣
t,4﹣![]() t),即:点G(
t),即:点G(![]() t,4﹣
t,4﹣![]() t),将点G(
t),将点G(![]() t,4﹣
t,4﹣![]() t)代入到抛物线得: 4﹣
t)代入到抛物线得: 4﹣![]() t=
t=![]() ,解得:t1=0(舍),t2=
,解得:t1=0(舍),t2=![]() .
.
答:当t=![]() 时,点G落在抛物线上;
时,点G落在抛物线上;
(3)如图2,连接BD,当G在BD上时, ![]() t=4,t=
t=4,t=![]() ,分三种情况讨论:
,分三种情况讨论:
①当0≤t≤![]() 时,如图3,过G作GH⊥x轴于H,延长HG交AB于M,则GM⊥AB,∵B(4,4),D(4,0),∴BD⊥x轴,∴S△BCG=S梯形GHDB+S△BDC﹣S△GHC,4=
时,如图3,过G作GH⊥x轴于H,延长HG交AB于M,则GM⊥AB,∵B(4,4),D(4,0),∴BD⊥x轴,∴S△BCG=S梯形GHDB+S△BDC﹣S△GHC,4=![]() (4﹣
(4﹣![]() t+4)(4﹣
t+4)(4﹣![]() t)+
t)+![]() ×4×(6﹣4)﹣
×4×(6﹣4)﹣![]() (6﹣
(6﹣![]() t)(4﹣
t)(4﹣![]() t),4=
t),4=![]() t,解得:t=
t,解得:t=![]() ,∴AM=
,∴AM=![]() t =
t =![]() ×
×![]() =
=![]() ,GM=
,GM=![]() t=
t=![]() ×
×![]() =
=![]() ,在Rt△AGM中,由勾股定理得:AG=
,在Rt△AGM中,由勾股定理得:AG=![]() =
= =
=![]() ;
;
∴当t=![]() 时,此时点G运动的路径长为
时,此时点G运动的路径长为![]() ;
;
②当G在BC上时,如图4,tan∠C=![]() =2,∴GH=2HC,∴4﹣
=2,∴GH=2HC,∴4﹣![]() t=2(6﹣
t=2(6﹣![]() t),t=
t),t=![]() ,当
,当![]() <t≤
<t≤![]() 时,如图5,S△BCG=S△BDC﹣S梯形BDHG﹣S△GHC,4=
时,如图5,S△BCG=S△BDC﹣S梯形BDHG﹣S△GHC,4=![]() ×4×2﹣
×4×2﹣![]() (4﹣
(4﹣![]() t+4)(
t+4)(![]() t﹣4)﹣
t﹣4)﹣![]() ×(4-
×(4-![]() t)(6-
t)(6-![]() t),t=
t),t=![]() (不在此范围内,不符合题意);
(不在此范围内,不符合题意);
③当E与D重合时,F与B重合,如图6,t=![]() =4,∴G(6,2),∴AG=
=4,∴G(6,2),∴AG=![]() =
=![]() ,∴S△BCG=S梯形BDCG﹣S△BDC=
,∴S△BCG=S梯形BDCG﹣S△BDC=![]() ×2×(4+2)﹣
×2×(4+2)﹣![]() ×2×4=2,∴当t>4时,如图7,由题意得:DE=t﹣4,∴OE=t﹣4+4=t,∴OH=OE+EH=t+2,EH=2,GM=GH=2,BM=t+2﹣4=t﹣2,CH=t+2﹣6=t﹣4,过G作MH⊥x轴,交x轴于H,交直线AB于M,∴S△BGC=S梯形BCHM﹣S△BGM﹣S△GCH,4=
×2×4=2,∴当t>4时,如图7,由题意得:DE=t﹣4,∴OE=t﹣4+4=t,∴OH=OE+EH=t+2,EH=2,GM=GH=2,BM=t+2﹣4=t﹣2,CH=t+2﹣6=t﹣4,过G作MH⊥x轴,交x轴于H,交直线AB于M,∴S△BGC=S梯形BCHM﹣S△BGM﹣S△GCH,4=![]() (t﹣4+t﹣2)×4﹣
(t﹣4+t﹣2)×4﹣![]() ×2×(t﹣2)﹣
×2×(t﹣2)﹣![]() ×2×(t﹣4),t=5,当t=5时,点G的运动路径分为两部分组成:
×2×(t﹣4),t=5,当t=5时,点G的运动路径分为两部分组成:
i)点G从A运动到D时,运动路径为:如图6中的AG长,即为![]() ;
;
ii)点G从D点继续在射线DC上运动1秒时,路径为1;
所以当t=5时,此时点G运动的路径长度为![]() .
.
综上所述:当t1=![]() 秒,此时路径长度为
秒,此时路径长度为![]() ,当t2=5秒,此时路径长度为
,当t2=5秒,此时路径长度为![]() .
.



-
科目: 来源: 题型:
查看答案和解析>>【题目】为帮助灾区人民重建家园,某校学生积极捐款.已知第一次捐款总额为9000元,第二次捐款总额为12000元,两次人均捐款额相等,但第二次捐款人数比第一次多50人.求该校第二次捐款的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A.无理数是开方开不尽的数
B.y 轴上的点,纵坐标为 0
C.邻补角一定互补
D.有且只有一条直线与已知直线垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3+a4=a7B.a3a6=a9C.2m5m=7mD.a3+a3=3a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,假分数可以化为带分数.例如:
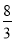 =2+
=2+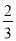 =2
=2 在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如: 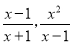 这样的分式就是假分式;
这样的分式就是假分式; 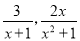 这样的分式就是真分式 .类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
这样的分式就是真分式 .类似的,假分式也可以化为带分式(即:整式与真分式和的形式).例如:
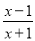 =
=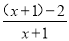 =1-
=1-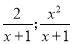 =
=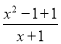 =
=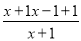 =
= 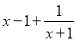

(1)将分式
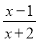 化为带分式;
化为带分式;(2)若分式
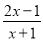 的值为整数,求x的整数值.
的值为整数,求x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点B位于y轴的左侧,到x轴的距离是4个单位长度,到y轴的距离是5个单位长度,则点B的坐标是( )
A.(﹣5,4)B.(﹣4,5)
C.(﹣5,4)或(﹣5,﹣4)D.(﹣4,5)或(﹣4,﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解.C.知道一点.D.完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题:
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率.

相关试题

