【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ= ![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
参考答案:
【答案】
(1)
解:∵OB=OC=6,
∴B(6,0),C(0,﹣6),
∴ 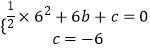 ,解得
,解得 ![]() ,
,
∴抛物线解析式为y= ![]() x2﹣2x﹣6,
x2﹣2x﹣6,
∵y= ![]() x2﹣2x﹣6=
x2﹣2x﹣6= ![]() (x﹣2)2﹣8,
(x﹣2)2﹣8,
∴点D的坐标为(2,﹣8);
(2)
解:如图1,过F作FG⊥x轴于点G,
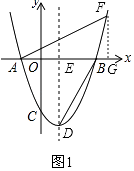
设F(x, ![]() x2﹣2x﹣6),则FG=|
x2﹣2x﹣6),则FG=| ![]() x2﹣2x﹣6|,
x2﹣2x﹣6|,
在y= ![]() x2﹣2x﹣6中,令y=0可得
x2﹣2x﹣6中,令y=0可得 ![]() x2﹣2x﹣6=0,解得x=﹣2或x=6,
x2﹣2x﹣6=0,解得x=﹣2或x=6,
∴A(﹣2,0),
∴OA=2,则AG=x+2,
∵B(6,0),D(2,﹣8),
∴BE=6﹣2=4,DE=8,
当∠FAB=∠EDB时,且∠FGA=∠BED,
∴△FAG∽△BDE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
当点F在x轴上方时,则有 ![]() =
= ![]() ,解得x=﹣2(舍去)或x=7,此进F点坐标为(7,
,解得x=﹣2(舍去)或x=7,此进F点坐标为(7, ![]() );
);
当点F在x轴上方时,则有 ![]() =﹣
=﹣ ![]() ,解得x=﹣2(舍去)或x=5,此进F点坐标为(5,﹣
,解得x=﹣2(舍去)或x=5,此进F点坐标为(5,﹣ ![]() );
);
综上可知F点的坐标为(7, ![]() )或(5,﹣
)或(5,﹣ ![]() );
);
(3)
解:∵点P在x轴上,
∴由菱形的对称性可知P(2,0),
如图2,当MN在x轴上方时,设T为菱形对角线的交点,
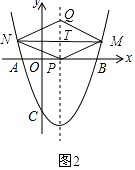
∵PQ= ![]() MN,
MN,
∴MT=2PT,
设PT=n,则MT=2n,
∴M(2+2n,n),
∵M在抛物线上,
∴n= ![]() (2+2n)2﹣2(2+2n)﹣6,解得n=
(2+2n)2﹣2(2+2n)﹣6,解得n= ![]() 或n=
或n= ![]() ,
,
∴MN=2MT=4n= ![]() +1;
+1;
当MN在x轴下方时,同理可设PT=n,则M(2+2n,﹣n),
∴﹣n= ![]() (2+2n)2﹣2(2+2n)﹣6,解得n=
(2+2n)2﹣2(2+2n)﹣6,解得n= ![]() 或n=
或n= ![]() (舍去),
(舍去),
∴MN=2MT=4n= ![]() ﹣1;
﹣1;
综上可知菱形对角线MN的长为 ![]() +1或
+1或 ![]() ﹣1.
﹣1.
【解析】(1)由条件可求得B、C坐标,利用待定系数法可求得抛物线解析式,进一步可求得D点坐标;(2)过F作FG⊥x轴于点G,可设出F点坐标,利用△FAG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,可求得F点的坐标;(3)可求得P点坐标,设T为菱形对角线的交点,设出PT的长为n,从而可表示出M点的坐标,代入抛物线解析式可得到n的方程,可求得n的值,从而可求得MN的长.
【考点精析】认真审题,首先需要了解相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.

(1)求证:DF是⊙O的切线;
(2)若AE=4,cosA= ,求DF的长.
,求DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.

(1)第24天的日销售量是件,日销售利润是元.
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】定义: 数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹);
(2)如图2,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用:
CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用: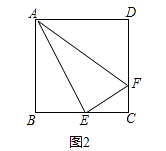
(3)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )

A. =
= 
B. =
= 
C. =
= 
D. =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( )

A.小涛家离报亭的距离是900m
B.小涛从家去报亭的平均速度是60m/min
C.小涛从报亭返回家中的平均速度是80m/min
D.小涛在报亭看报用了15min -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=
 ,则CE的长为 .
,则CE的长为 .
相关试题

