【题目】周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( ) 
A.小涛家离报亭的距离是900m
B.小涛从家去报亭的平均速度是60m/min
C.小涛从报亭返回家中的平均速度是80m/min
D.小涛在报亭看报用了15min
参考答案:
【答案】D
【解析】解:A、由纵坐标看出小涛家离报亭的距离是1200m,故A不符合题意; B、由纵坐标看出小涛家离报亭的距离是1200m,由横坐标看出小涛去报亭用了15分钟,小涛从家去报亭的平均速度是80m/min,故B不符合题意;
C、返回时的解析式为y=﹣60x+3000,当y=1200时,x=30,由横坐标看出返回时的时间是50﹣30=20min,返回时的速度是1200÷20=60m/min,故C不符合题意;
D、由横坐标看出小涛在报亭看报用了30﹣15=15min,故D符合题意;
故选:D.
【考点精析】掌握函数的图象是解答本题的根本,需要知道函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义: 数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹);
(2)如图2,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用:
CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用: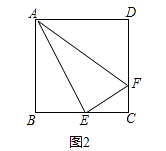
(3)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ= MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )

A. =
= 
B. =
= 
C. =
= 
D. =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=
 ,则CE的长为 .
,则CE的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.

(1)在图中画出以AB为底、面积为12的等腰△ABC,且点C在小正方形的顶点上;
(2)在图中画出平行四边形ABDE,且点D和点E均在小正方形的顶点上,tan∠EAB= ,连接CD,请直接写出线段CD的长.
,连接CD,请直接写出线段CD的长.
相关试题

