【题目】如图,圆的周长为4个单位长度,在圆的四等分点处标上字母![]() ,先将圆周上的字母
,先将圆周上的字母![]() 对应的点与数轴的数字0对应的点重合,若将圆沿着数轴向左滚动,那么数轴上的-2019所对应的的点将与圆周上字母__________所对应的的点重合.
对应的点与数轴的数字0对应的点重合,若将圆沿着数轴向左滚动,那么数轴上的-2019所对应的的点将与圆周上字母__________所对应的的点重合.

参考答案:
【答案】D
【解析】
因为圆沿着数轴向左滚动,依次与数轴上数字顺序重合的是A、B、C、D、A,…,且A点只与4的倍数点重合,即数轴上表示-4n的点都与A点重合,表示-4n-1的数都与B点重合,表示-4n-2的数都与C点重合,表示-4n-3的数都与D点重合,依此按序类推可得出结果.
解:设数轴上的一个整数为x,由题意可知
当x=-4n时(n≥0且n为整数),A点与x重合;
当x=-4n-1时(n≥0且n为整数),B点与x重合;
当x=-4n-2时(n≥0且n为整数),C点与x重合;
当x=-4n-3时(n≥0且n为整数),D点与x重合;
而-2019=-504×4-3,所以数轴上的-2019所对应的点与圆周上字母D重合.
故答案为:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 的角平分线
的角平分线 交于
交于 于点
于点 ,点
,点 为
为 上一点,且
上一点,且 ,
, ,
, 交于点
交于点 .
.
(1)求
 的度数;
的度数;(2)若
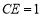 ,求
,求 的长度
的长度(3)若
 于点
于点 ,证明:
,证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由
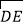 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.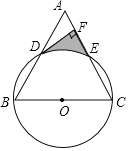
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=
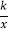 (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
相关试题

