【题目】如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N﹣M,Q(t)=M+N.
(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
参考答案:
【答案】
(1)解:设“阶梯数”t的百位为x,相邻两数的差为k,则t= ![]() ,
,
∴M=a+a=2a,N=a+k,
∴P(t)=2N﹣M=2(a+k)﹣2a=2k=12,
∴k=6,
∵Q(t)=M+N=2a+a+k=3a+6为一个完全平方数,其中1≤a≤9,
∴9≤3a+6≤33,
∴3a+6=9,16,25,
∴a=1,
∴t=171;
(2)解:设某五位阶梯数为 ![]() ,
,
∵ ![]() =
= ![]() =2778a+302k+
=2778a+302k+ ![]() ,
,
∴2k﹣a是4的倍数,
∵M=3a+2k,N=2A+2K,
∴Q(t)=M+N=5a+4k,
∴ ![]() =k+a+
=k+a+ ![]() ,
,
∴a﹣2是4的倍数,
∵1≤a≤9,
∴﹣1≤a﹣2≤7,
∴a﹣2=0,4,
∴a=2,6
当a=2时, ![]() 为整数且0≤2+2k≤9,
为整数且0≤2+2k≤9,
∴﹣1≤k≤ ![]() ,
,
∴k=±1,3,
所以t=21012,23432,25852;
当a=6时, ![]() 为整数且0≤6+2k≤9,
为整数且0≤6+2k≤9,
∴﹣3≤k≤ ![]() ,
,
∴k=±1,﹣3,
所以t=63036,65456,67876.
所以该五位“阶梯数”t的最大值是67876,最小值是21012.
【解析】(1)设“阶梯数”t的百位为x,相邻两数的差为k,则t= a ( a + k ) a ,可得M=a+a=2a,N=a+k,根据P(t)=12,得到关于k的方程,可求得k=6,再根据Q(t)=3a+6为一个完全平方数,其中1≤a≤9,可求3a+6=9,16,25,可求a=1,从而得到这个三位数;
(2)设某五位阶梯数为 a ( a + k ) ( a + 2 k ) ( a + k ) a ,根据 ![]() =
= ![]() =2778a+302k+
=2778a+302k+ ![]() ,可得2k﹣a是4的倍数,根据M=3a+2k,N=2A+2K,可得Q(t)=M+N=5a+4k,则
,可得2k﹣a是4的倍数,根据M=3a+2k,N=2A+2K,可得Q(t)=M+N=5a+4k,则![]() =k+a+
=k+a+![]() ,可得a﹣2是4的倍数,根据完全平方数的定义得到a=2,6,再分两种情况求出T的值,进一步得到该五位“阶梯数”t的最大值和最小值。
,可得a﹣2是4的倍数,根据完全平方数的定义得到a=2,6,再分两种情况求出T的值,进一步得到该五位“阶梯数”t的最大值和最小值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度在圆周的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴上的原点重合,再将圆沿着数轴向右滚动,那么数轴上的1949所对应的点与圆周上字母
 所对应的点重合.
所对应的点重合.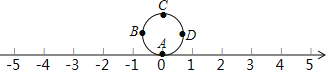
A. AB. BC. CD. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
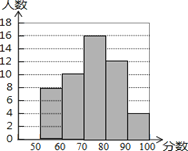
(1)本次选取参加测试的学生人数是 ___;
(2)学生“信息素养”得分的中位数落在 _____;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学
生的平均分为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解学生参加体育运动的兴趣情况,从全校学生中随机抽取部分学生进行调查,对样本数据整理后画出如下统计图统计图不够完整请结合图中信息解答下列问题:
 此样本的样本容量为:______;
此样本的样本容量为:______; 补全条形统计图;
补全条形统计图; 求兴趣为“中”的学生所占的百分比以及对应扇形的圆心角.
求兴趣为“中”的学生所占的百分比以及对应扇形的圆心角.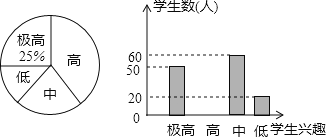
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A表示的数为
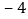 ,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动
,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动 设运动时间为t秒
设运动时间为t秒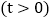 .
.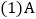 ,B两点间的距离等于______,线段AB的中点表示的数为______;
,B两点间的距离等于______,线段AB的中点表示的数为______;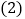 用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;
用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______; 求当t为何值时,
求当t为何值时,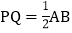 ?
? 若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

相关试题

