【题目】完成下面的证明:
已知:如图,D是BC上任意一点,BE⊥AD,交AD的延长线于点E,CF⊥AD,垂足为F.
求证:∠1=∠2.
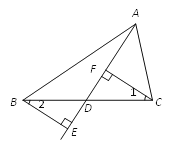
证明:∵ BE⊥AD(已知),
∴ ∠BED= °( ).
又∵ CF⊥AD(已知),
∴ ∠CFD= °.
∴ ∠BED=∠CFD(等量代换).
∴ BE∥CF( ).
∴ ∠1=∠2( ).
参考答案:
【答案】证明见解析
【解析】试题分析:由BE垂直于AD,利用垂直的定义得到∠BED为直角,再由CF垂直于AD,得到∠CFD为直角,得到一对内错角相等,进而确定出BE与CF平行,利用两直线平行内错角相等即可得证.
试题解析:∴∠BED=90°(垂直定义),
∵CF⊥AD,
∴∠CFD=90°,
∴∠BED=∠CFD,
∴BE∥CF(内错角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等).
故答案为:90;垂直的定义;90;内错角相等,两直线平行;两直线平行,内错角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用________,可以很准确地表示出一个位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】频数分布直方图反映了( )
A. 样本数据的多少 B. 样本数据的平均水平
C. 样本数据所分组数 D. 样本数据在各组的频数分布情况
-
科目: 来源: 题型:
查看答案和解析>>【题目】2的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
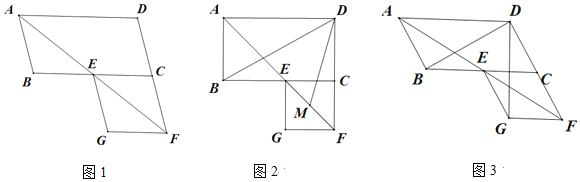
-
科目: 来源: 题型:
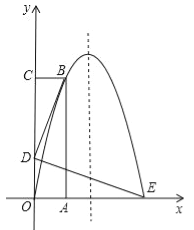
查看答案和解析>>【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点。当△APB为直角三角形时,AP= .
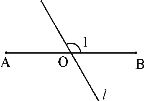
相关试题

