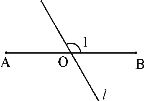
【题目】如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点。当△APB为直角三角形时,AP= .
参考答案:
【答案】3或3![]() 或3
或3![]() .
.
【解析】
试题分析:分以一下情况讨论:
(1)在Rt△A P1B中,∵∠1=120°,O P1=OB,∴∠O B P1 =∠O P1B=30°,∴AP1 =![]() AB=
AB=![]() ×6=3;
×6=3;
(2)在Rt△A P2B中,∵∠1=120°,O P2=OB,∴∠P2 B O =∠O P2B=60°,∴AP2 =![]() AB=cos∠O B P2×6=
AB=cos∠O B P2×6=![]() ×6=3
×6=3![]() ;
;
(3)P3B为以B为切点的⊙O的切线,∵∠1=120°,O P2=OB,∴∠P2 B O =∠O P2B=60°,∴∠P3O B=60°,在Rt△O P3B中,∴BP3 =tan∠P3O B×3 =![]() ×3=3
×3=3![]() ;在Rt△A P3B中,AP3 =
;在Rt△A P3B中,AP3 =![]() =
=![]() =3
=3![]() ;
;
(4)P4B为以A为切点的⊙O的切线,∵∠1=120°,O P1=OA,∴∠P1 A O =∠O P1A=60°,∴∠P4O A=60°,在Rt△O P4A中,∴AP4 =tan∠P4O A×3 =![]() ×3=3
×3=3![]() .
.
综上,当△APB为直角三角形时,AP=3,或3![]() ,或3
,或3![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
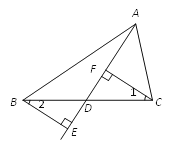
已知:如图,D是BC上任意一点,BE⊥AD,交AD的延长线于点E,CF⊥AD,垂足为F.
求证:∠1=∠2.
证明:∵ BE⊥AD(已知),
∴ ∠BED= °( ).
又∵ CF⊥AD(已知),
∴ ∠CFD= °.
∴ ∠BED=∠CFD(等量代换).
∴ BE∥CF( ).
∴ ∠1=∠2( ).
-
科目: 来源: 题型:
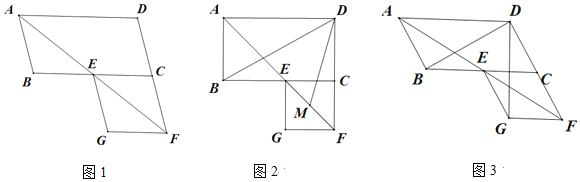
查看答案和解析>>【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
-
科目: 来源: 题型:
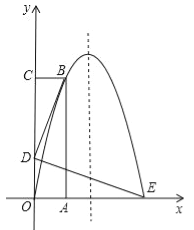
查看答案和解析>>【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查,每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如下两幅不完整的统计图.
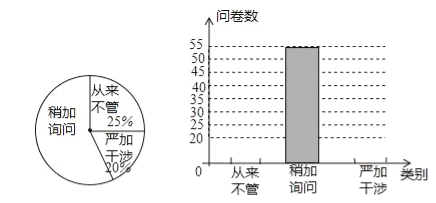
(1)“从来不管”的问卷有 份,在扇形图中“严加干涉”的问卷对应的圆心角为 .
(2)请把条形图补充完整.
(3)若该校共有学生2000名,请估计该校对手机问题“严加干涉”的家长有多少人.
-
科目: 来源: 题型:
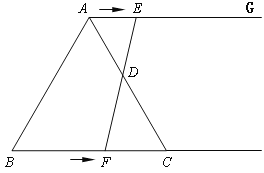
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空:当t为_________s时,四边形ACFE是菱形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
相关试题

