【题目】平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a![]() ,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)求点P(﹣2,3)的“2关联点”P′的坐标;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,6),求出k及点P的坐标;
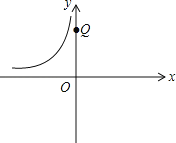
(3)如图,点Q的坐标为(0,4![]() ),点A在函数y=﹣
),点A在函数y=﹣![]() (x<0)的图象上运动,且点A是点B的“﹣
(x<0)的图象上运动,且点A是点B的“﹣![]() 关联点”,当线段BQ最短时,求B点坐标.
关联点”,当线段BQ最短时,求B点坐标.
参考答案:
【答案】(1)P′(﹣![]() ,﹣1);(2)k=2,P′(1,4)、(2,2);(3)B(
,﹣1);(2)k=2,P′(1,4)、(2,2);(3)B(![]() ,
,![]()
![]() ).
).
【解析】
试题分析:(1)根据题中的新定义求出点P(﹣2,3)的“2关联点”P′的坐标即可;
(2)根据题中的新定义求出a与b的关系式即可;
(3)根据题意得出A(a﹣![]() ,﹣
,﹣![]() a+b),代入y=﹣
a+b),代入y=﹣![]() (x<0),求得b=
(x<0),求得b=![]() a+2
a+2![]() ,从而求得B在直线y=
,从而求得B在直线y=![]() x+2
x+2![]() 上,过Q作y=
上,过Q作y=![]() x+2
x+2![]() 的垂线QB1,垂足为B1,Q(0,4
的垂线QB1,垂足为B1,Q(0,4![]() ),且线段BQ最短,B1即为所求的B点,由△MB1Q∽△MON 得
),且线段BQ最短,B1即为所求的B点,由△MB1Q∽△MON 得![]() =
=![]() =
=![]() ,由ON=2,OM=2
,由ON=2,OM=2![]() ,根据勾股定理求得MN=4.由MQ=2
,根据勾股定理求得MN=4.由MQ=2![]() ,求得B1Q=
,求得B1Q=![]() ,MB1=3,在Rt△MB1Q中,根据面积公式得到B1QMB1=MQhB1,即可求得B的坐标.
,MB1=3,在Rt△MB1Q中,根据面积公式得到B1QMB1=MQhB1,即可求得B的坐标.
解:(1)∵x=﹣2+![]() =﹣
=﹣![]() ,y=2×(﹣2)+3=﹣1,
,y=2×(﹣2)+3=﹣1,
∴P′(﹣![]() ,﹣1);
,﹣1);
(2)设P(a,b),则P′(a+![]() ,ka+b)
,ka+b)
∴ ,
,
∴k=2,
∴2a+b=6.
∵a、b为正整数
∴P′(1,4)、(2,2);
(3)∵B的“﹣![]() 关联点”是A,
关联点”是A,
∴A(a﹣![]() ,﹣
,﹣![]() a+b),
a+b),
∵点A还在反比例函数y=﹣![]() 的图象上,
的图象上,
∴(﹣![]() a+b)(a﹣
a+b)(a﹣![]() )=﹣4
)=﹣4![]() ,
,
∴(b﹣![]() a)2=12,
a)2=12,
∵b﹣![]() a>0,
a>0,
∴b﹣![]() a=2
a=2![]() ,
,
∴b=![]() a+2
a+2![]() ;
;
∴B在直线y=![]() x+2
x+2![]() 上.
上.
过Q作y=![]() x+2
x+2![]() 的垂线QB1,垂足为B1,
的垂线QB1,垂足为B1,
∵Q(0,4![]() ),且线段BQ最短,
),且线段BQ最短,
∴B1即为所求的B点,
由△MB1Q∽△MON 得![]() =
=![]() =
=![]() ,
,
∵ON=2,OM=2![]() ,
,
∴MN=4.
又∵MQ=2![]() ,
,
∴B1Q=![]() ,MB1=3
,MB1=3
在Rt△MB1Q中,B1QMB1=MQhB1,
∴hB1=![]() ,
,
∴xB1=![]() ,
,
∴B(![]() ,
,![]()
![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(-2ab)(3a2-2ab-b2)
(2)用乘法公式计算:102×98
(3)计算:2(m+1)2-(2m+1)(2m-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A ( 5, 3 ) 的坐标变为 ( 3 , -1),则点A经历了怎样的图形变化 ( )
A .先向左平移2个单位长度,再向下平移4个单位长度
B. 先向左平移2个单位长度,再向上平移4个单位长度
C. 先向右平移2个单位长度,再向上平移4个单位长度
D. 先向右平移2个单位长度,再向下平移4个单位长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的等边△ACB中,E是对称轴AD上一个动点,连EC,将线段EC绕点C逆时针旋转60°得到MC,连DM,则在点E运动过程中,DM的最小值是_____。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,-5)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200×2x=1000
C.200+200×3x=1000
D.200[1+(1+x)+(1+x)2]=1000
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连结OA,二次函数y=x2图象从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
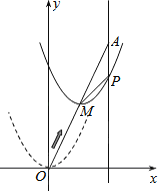
(1)求线段OA所在直线的函数解析式;
(2)设二次函数顶点M的横坐标为m,当m为何值时,线段PB最短,并求出二次函数的表达式;
(3)当线段PB最短时,二次函数的图象是否过点Q(a,a﹣1),并说理由.
相关试题

