【题目】如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数![]() 的图象有一个交点为A(m,2).
的图象有一个交点为A(m,2).
(1)求m的值及正比例函数y=kx的表达式;
(2)试判断点B(2,3)是否在正比例函数图象上,并说明理由.

参考答案:
【答案】 (1)m=1,正比例函数的表达式为y=2x;(2)点B(2,3)不在正比例函数图象上,理由见解析.
【解析】试题分析:(1)将A(m,2)点代入反比例函数y= y=![]() ,即可求得m的值;
,即可求得m的值;
(2)将A点坐标代入正比例函数y=kx,即可求得正比例函数的解析式;
(3)将x=2代入(2)中所求的正比例函数的解析式,求出对应的y值,然后与3比较,如果y=3,那么点B(2,3)是否在正比例函数图象上;否则不在.
试题解析:(1)把A(m,2) 代入反比例函数表达式y=![]() ,
,
得2=![]() ,所以m=1.
,所以m=1.
把A(1,2) 代入正比例函数表达式y=kx,
得2=k,
所以k=2.
因此正比例函数的表达式为y=2x;
(2)因为正比例函数的表达式为y=2x,当x=2时,y=4≠3,所以点B(2,3)不在正比例函数图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若
 是
是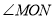 的平分线
的平分线 上一点,点
上一点,点 在
在 上,此时,在
上,此时,在 截取
截取 ,连接
,连接 ,根据三角形全等的判定
,根据三角形全等的判定 ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿ 和⊿
和⊿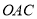 ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:
如图2,在非等边⊿
 中,
中,  ,
,  分别是
分别是 的平分线,且
的平分线,且 交于点
交于点 .求证:
.求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于自然数的等式:
a1:32-12=8×1;
a2:52-32=8×2;
a3:72-52=8×3;……
根据上述规律解决下列问题:
⑴写出第a4个等式:___________;
⑵写出你猜想的第an个等式(用含n的式子表示),并验证其正确性;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小刚一起玩抛掷两枚硬币的游戏,游戏规则:抛出两个正面--小明赢1分;抛出其他结果--小刚赢1分;谁先到10分,谁就获胜.这是个不公平的游戏规则,要把它修改成公平的游戏,下列做法中错误的是( )
A. 把“抛出两个正面”改为“抛出两个同面”
B. 把“抛出其他结果”改为“抛出两个反面”
C. 把“小明赢1分”改为“小明赢3分”
D. 把“小刚赢1分”改为“小刚赢3分”
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称
特征点的个数
图1
7
图2
12
…
…
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.
相关试题

