【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .

参考答案:
【答案】(1)![]() ;(2)图见解析;(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;(4)(﹣2x﹣2,2y+2).
;(2)图见解析;(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;(4)(﹣2x﹣2,2y+2).
【解析】试题分析:(1)根据位似图形可得位似比即可;(2)根据轴对称图形的画法画出图形即可;(3)根据△A3B3C3与△A2B2C2的关系过程其变化过程即可;(4)根据三次变换规律得出坐标即可.
试题解析:(1))△ABC与△A1B1C1的位似比等于=![]() ;
;
(2)如图所示
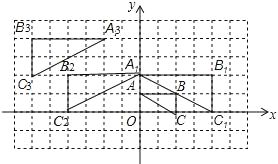
(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;
(4)点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为(﹣2x﹣2,2y+2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数
 的图象有一个交点为A(m,2).
的图象有一个交点为A(m,2).(1)求m的值及正比例函数y=kx的表达式;
(2)试判断点B(2,3)是否在正比例函数图象上,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小刚一起玩抛掷两枚硬币的游戏,游戏规则:抛出两个正面--小明赢1分;抛出其他结果--小刚赢1分;谁先到10分,谁就获胜.这是个不公平的游戏规则,要把它修改成公平的游戏,下列做法中错误的是( )
A. 把“抛出两个正面”改为“抛出两个同面”
B. 把“抛出其他结果”改为“抛出两个反面”
C. 把“小明赢1分”改为“小明赢3分”
D. 把“小刚赢1分”改为“小刚赢3分”
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称
特征点的个数
图1
7
图2
12
…
…
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张形状、大小和质地完全相同的卡片,每张卡片的正面写有一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.则抽取的两张卡片上的算式都正确的概率是( )

A.
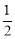 B.
B.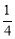 C.
C.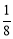 D.
D. 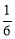
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先从简单的情形入手:
分别计算下列各式的值:
①(x-1)(x+1)=x2-1;
②(x-1)(x2+x+1)=x3-1;
③(x-1)(x3+x2+x+1)=x4-1;…
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________;
请你利用上面的结论,完成下面三题的计算:
⑴299+298+297+…+2+1;
⑵(-2)50+(-2)49+(-2)48+…+(-2)+1
⑶已知
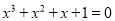 ,求
,求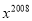 的值.
的值.
相关试题

