Question

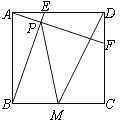
【题目】如图，正方形ABCD中，AB=4，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为．

Answer 1

【答案】2.

【解析】

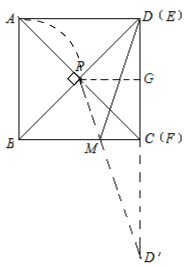
试题分析：本题主要考查的是最短路径问题，由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.首先作出点D关于BC的对称点D′，从而可知当点P、M、D′在一条直线上时，路径最短，当点E与点D重合，点F与点C重合时，PG和GD′均最短，即PD′最短，然后由正方形的性质和轴对称图形的性质可知：PG=2，GD′=6，最后由勾股定理即可求得PD′的长，从而可求得MD+MP的最小值.

如图作点D关于BC的对称点D′，连接PD′，由轴对称的性质可知：MD=D′M，CD=CD′=4,

∴PM+DM=PM+MD′=PD′，过点P作PG垂直于C，垂足为G，易证AF⊥BE，故可知P的轨迹为以AB为直径的四分之一圆弧，当点E与点D重合，点F与点C重合时，PG和GD′均最短， ∴此时PD′最短．

∵四边形ABCD为正方形，

∴PG=AD=2，GC=DC=2．

∴GD′=6．

在Rt△PGD′中，由勾股定理得：PD′==＝2．

故答案为2.