【题目】已知一次函数y=(m+2)x+3-n,
(l)m,n是何值时,y随x的增大而减小?
(2)m,n为何值时,函数的图象经过原点?
(3)若函数图象经过第二、三、四象限,求 m,n的取值范围.
参考答案:
【答案】(1)m<-2,n为任意实数时,y随x的增大而减小;(2)当m≠-2且n=3时,图象经过原点;(3)当m<-2且n>3时,函数图象经过第二、三、四象限.
【解析】试题分析:(1)根据一次函数的性质可得m+2<0,对其求解即可;
(2)结合题意可知一次函数是正比例函数,此时结合正比例函数的定义进行解答即可;
(3)根据一次函数的性质列出不等式组,并进行解答即可.
试题解析:
1)由题意得:m+2<0,
∴m<-2,
∴m<-2,n为任意实数时,y随x的增大而减小。
(2)由题意得:m+2≠0且3-n=0,
∴m≠-2且n=3,
∴当m≠-2且n=3时,图象经过原点。
(3)由题意得: ![]() ,
,
得: ![]()
∴当m<-2且n>3时,函数图象经过第二、三、四象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.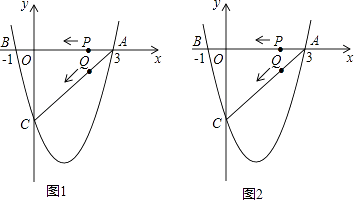
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折线ABCDE描述了一辆汽车在某一直线上行驶过程中,汽车离出发地的距离y(km)和行驶时间x(h)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120km;②汽车在行驶途中停留了0.5h;③汽车在整个行驶过程中的平均速度为
 km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)
km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
①若单项式﹣xmyn+4 与 5x2y 是同类项,则 nm 的值为____.
②实施西部大开发战略是党中央的重大决策,我国国土面积约为960 万平方千米,而我国西部地区的面积占我国国土面积的
 ,用科学记数法表示我国西部地区的面积约为_____平方千米.
,用科学记数法表示我国西部地区的面积约为_____平方千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形正六边形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是( )
A.
B.
C.
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0,y1(元)与正常运营时间x(天)之间分别满足关系式:y0=ax,y1=b+50x,图象如图所示.
(1)每辆车改装前每天的燃料费a= 元,每辆车的改装费b= 元,正常运营时间 天后,就可以从节省的燃料费中收回改装成本;
(2)某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费40万元?
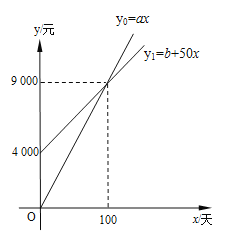
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )

A.150°
B.210°
C.105°
D.75°
相关试题

