【题目】如图,从①![]() ,②
,②![]() ,③
,③![]() 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.

(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
参考答案:
【答案】(1)3;(2)(答案不唯一)选①②为条件,③为结论,证明见解析
【解析】
(1)先得出所有的情况,再根据平行线的判定和性质即可得出答案;
(2)选①②为条件,③为结论,如图所示.易得![]() ,则DB∥EC,然后利用平行线的性质和已知可得
,则DB∥EC,然后利用平行线的性质和已知可得![]() ,于是有DF∥AC,进而可得结论.
,于是有DF∥AC,进而可得结论.
解:(1)由①②,得③;由①③,得②;由②③,得①;均为真命题,故答案为3;
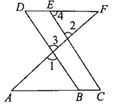
(2)(答案不唯一)选①②为条件,③为结论,如图所示:
![]() (已知),
(已知),![]() (对顶角相等),
(对顶角相等),
![]() (等量代换),
(等量代换),
![]() (同位角相等,两直线平行),
(同位角相等,两直线平行),
![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).
∵![]() (已知),
(已知),
![]() (等量代换),
(等量代换),
![]() (内错角相等,两直线平行),
(内错角相等,两直线平行),
![]() (两直线平行,内错角相等).
(两直线平行,内错角相等).
-
科目: 来源: 题型:
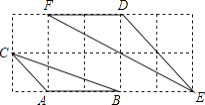
查看答案和解析>>【题目】如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△DEF:S△ABC的值为 .
-
科目: 来源: 题型:
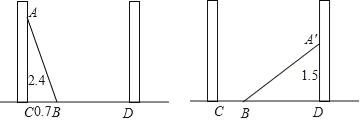
查看答案和解析>>【题目】如图,小巷左石两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,求小巷有多宽.
-
科目: 来源: 题型:
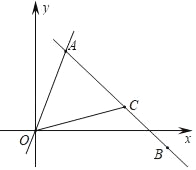
查看答案和解析>>【题目】如图,直线OA与直线BC相交于点A,且点B的坐标为(5,﹣1),点C的坐标为(3,1),直线OA的解析式为y=3x
(1)求直线BC的解析式;
(2)求点A的坐标;
(3)求△OAC的面积.
-
科目: 来源: 题型:
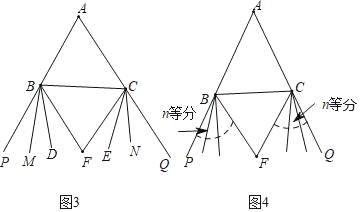
查看答案和解析>>【题目】(1)如图1,已知△ABC,BF平分外角∠CBP,CF平分外角∠BCQ.试确定∠A和∠F的数量关系;
(2)如图2,已知△ABC,BF和BD三等分外角∠CBP,CF和CE三等分外角∠BCQ.试确定∠A和∠F的数量关系;
(3)如图3,已知△ABC,BF、BD和BM四等分外角∠CBP,CF、CE和CN四等分外角∠BCQ.试确定∠A和∠F的数量关系;
(4)如图4,已知△ABC,将外角∠CBP进行n等分,BF是临近BC边的等分线,将外角∠BCQ进行n等分,CF是临近BC边的等分线,试确定∠A和∠F的数量关系.

-
科目: 来源: 题型:
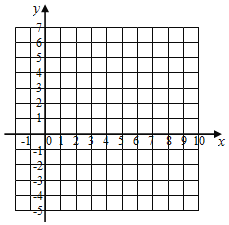
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(6,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2+
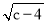 =0,
=0,(1)求A.B.C的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使三角形APC的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=
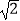 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 . 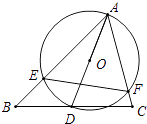
相关试题

