【题目】如图,甲,乙两军区进行军事演练,乙军区在河东岸![]() 处,因不知河宽,甲军的狙击手在
处,因不知河宽,甲军的狙击手在![]() 处很难瞄准乙军军营,于是甲军连长站在西岸的点
处很难瞄准乙军军营,于是甲军连长站在西岸的点![]() 处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营
处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营![]() 处,然后他后退到
处,然后他后退到![]() 点,这时他的视点恰好落在
点,这时他的视点恰好落在![]() 处,此时他只需测量脚站的
处,此时他只需测量脚站的![]() 点和
点和![]() 点的距高,即可知道狙击手与乙军军营的距离,他判断的依据是( )
点的距高,即可知道狙击手与乙军军营的距离,他判断的依据是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
根据身高不变可得AB=PO,视线方向不变可得∠AOB=∠PQO,然后利用“AAS”证明△ABO和△POQ全等,根据全等三角形对应边相等可得BO=OQ,从而即可知道狙击手与乙军军营的距离.
解:根据题意知AB=PO,AO∥PQ,
∴∠AOB=∠PQO,
又∵AB⊥BO,PO⊥BQ,
∴∠ABO=∠POQ=90°,
在△ABO和△POQ中,
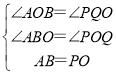 ,
,
∴△ABO≌△POQ(AAS),
∴BO=OQ,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张如图1的长方形铁皮,四个角都剪去边长为
 的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是
的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是 ,宽是
,宽是 这个无盖铁盒各个面的面积之和称为铁盒的全面积.
这个无盖铁盒各个面的面积之和称为铁盒的全面积.
(1)图1中原长方形铁皮的面积为_
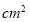 ;(用
;(用 的代数式表示)
的代数式表示)(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可涂的面积为
 ,则涂完这个铁盒需要多少钱?(用
,则涂完这个铁盒需要多少钱?(用 的代数式表示)
的代数式表示)(3)是否存在一个最大正整数
 ,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个
,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个 ,若不存在,请说明理由.
,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:对任意一个三位数
 如果
如果 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与 的商记为
的商记为 .例如
.例如 对调百位与十位上的数字得到
对调百位与十位上的数字得到 对调百位与个位上的数字得到
对调百位与个位上的数字得到 对调十位与个位上的数字得到
对调十位与个位上的数字得到 这三个新三位数的和为
这三个新三位数的和为 所以
所以 .试根据以上信息,完成下列问题:
.试根据以上信息,完成下列问题:(1)计算:
 __,
__, __,你从中发现什么规律?你发现规律是:__.
__,你从中发现什么规律?你发现规律是:__.(2)若
 都是“相异数”,
都是“相异数”,
 ,其中x是正整数),是否存在
,其中x是正整数),是否存在 满足
满足 ,若存在,请求出这个
,若存在,请求出这个 ,若不存在,请说明理由.
,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如下图.
请你根据统计图中的信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)该校学生最喜欢借阅哪类图书?
(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?
(无原图)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的一条中线,
的一条中线, 为
为 边上一点且
边上一点且 相交于
相交于 四边形
四边形 的面积为
的面积为 ,则
,则 的面积是( )
的面积是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 三个城市在同一直线上(
三个城市在同一直线上( 市在
市在 两市之间),甲、乙两车分别从
两市之间),甲、乙两车分别从 市、
市、 市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达
市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达 市时,甲、乙两车都停止运动,甲、乙两车到
市时,甲、乙两车都停止运动,甲、乙两车到 市的距离之和
市的距离之和 (千米)与甲车行驶的时间
(千米)与甲车行驶的时间 (小时)之间的关系如图所示,则当乙车到达
(小时)之间的关系如图所示,则当乙车到达 市时,甲车离
市时,甲车离 市还有_______千米.
市还有_______千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到
 .
.
(1)画出平移后的
 ;
; (2)写出
 三个顶点的坐标;
三个顶点的坐标;(3)已知点P在x轴上,以
 、
、 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标.
相关试题

