【题目】我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.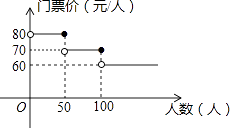
(1)求W关于x的函数关系式,并写出自变量x的取值范围;
(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;
(3)“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.
参考答案:
【答案】
(1)解:∵甲团队人数为x人,乙团队人数不超过50人,
∴120﹣x≤50,
∴x≥70,
①当70≤x≤100时,W=70x+80(120﹣x)=﹣10x+9600,
②当100<x<120时,W=60x+80(120﹣x)=﹣20x+9600,
综上所述,W= ![]()
(2)解:∵甲团队人数不超过100人,
∴x≤100,
∴W=﹣10x+9600,
∵70≤x≤100,
∴x=70时,W最大=8900(元),
两团联合购票需120×60=7200(元),
∴最多可节约8900﹣7200=1700(元)
(3)解:∵x≤100,
∴W=(70﹣a)x+80(120﹣x)=﹣(a+10)x+9600,
∴x=70时,W最大=﹣70a+8900(元),
两团联合购票需120(60﹣2a)=7200﹣240a(元),
∵﹣70a+8900﹣(7200﹣240a)=3400,
解得:a=10
【解析】(1)根据题意可得到甲团队人数大于等于70,然后再分为70≤x≤100和100<x<120两种情况求解即可;
(2)由题意可知x≤100,则W=-10x+9600(70≤x≤100)然后再利用一次函数的图象和性质求得W的最大值即可;
(3)由每张门票降价a元,可得到W=(70-a)x+80(120-x)=-(a+10)x+9600,由一次函数的增减性可知:x=70时,W最大=-70a+8900(元),接下来,再求得两队团联合购票所需的费用,最后,依据甲乙两团队联合购票比分别购票最多节约3400元列方程求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位,再向下平移4个长度单位得到点C.
(1)用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
(2)若t=1时,平移线段AB,使点A、B到坐标轴上的点
 、
、 处,指出平移的方向和距离,并求出点
处,指出平移的方向和距离,并求出点 、
、 的坐标;
的坐标;(3)若t=0时,平移线段AB至MN(点A与点M对应),使点M落在x轴的负半轴上,三角形MNB的面积为4,试求点M、N的坐标.
-
科目: 来源: 题型:
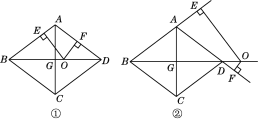
查看答案和解析>>【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
-
科目: 来源: 题型:
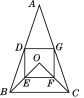
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点O在△ABC的内部,∠BOC=90°,OB=OC,D,E,F,G分别是AB,OB,OC,AC的中点.
(1)求证:四边形DEFG是矩形;
(2)若DE=2,EF=3,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若SΔABC=18,△ADF的面积为
 ,△CFE的面积为
,△CFE的面积为 ,则
,则
 =________
=________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y,z是三个非负数,并且满足x+2y-5z=6,2x+y+5z=9.设k=3x+y+5z,记a为k的最大值,b为k的最小值,试求ab的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车.经市场调查得知,购买6辆男式单车与8辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16 000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单车比女式单车多5辆,两种单车至少需要22辆,购置两种单车的费用不超过50 000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
相关试题

