【题目】下列结论错误的是( )
A.全等三角形对应边上的中线相等
B.两个直角三角形中,两个锐角相等,则这两个三角形全等
C.全等三角形对应边上的高相等
D.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
参考答案:
【答案】B
【解析】
试题分析:画出图形,根据全等三角形的性质和判定(全等三角形的判定定理有SAS,ASA,AAS,SSS)判断即可.
解: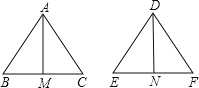
A、∵△ABC≌△DEF,
∴AB=DE,∠B=∠E,BC=EF,
∵AM是△ABC的中线,DN是△DEF中线,
∴BC=2BM,EF=2EN,
∴BM=EN,
在△ABM和△DEN中
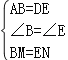
∴△ABM≌△DEN(SAS),
∴AM=DN,正确,故本选项错误;
B、如教师用得含30度的三角板和学生用的含30度的三角板就不全等,错误,故本选项正确;
C、
∵△ABC≌△DEF,
∴AB=DE,∠B=∠E,
∵AM是△ABC的高,DN是△DEF的高,
∴∠AMB=∠DNE=90°,
在△ABM和△DEN中
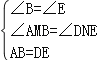
∴△ABM≌△DEN,
∴AM=DN,正确,故本选项错误;
D、根据AAS即可推出两直角三角形全等,正确,故本选项错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个系数为﹣7,且只含有x,y的四次单项式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.
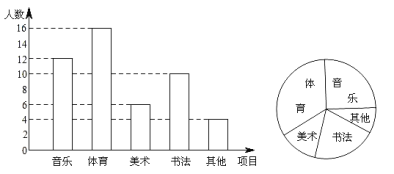
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)4﹣(﹣2)﹣2﹣32÷(3.14﹣π)0
(2)(3
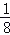 )12×(
)12×(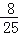 )11×(一2)3
)11×(一2)3(3)5a(a2﹣3a+1)﹣a2(1﹣a)
(4)(﹣a)3(﹣2ab2)3﹣4ab2(a5b4﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
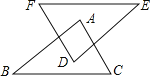
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了6位战士,发现前面的人数和后面的人数一样.
(1)这列队伍一共有多少名战士?
(2)这列队伍要过一座320米的大桥,为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒,从第一位战士刚上桥到全体通过大桥用了100秒时间,请问相邻两个战士间距离为多少米(不考虑战士身材的大小)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
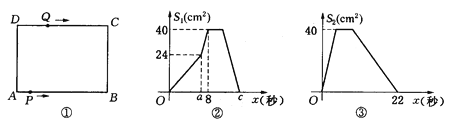
(1)、参照图象,求b、图②中c及d的值;
(2)、连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)、当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)、若点P、点Q在运动路线上相距的路程为25cm,求x的值.
相关试题

