【题目】如图,ABCD中,点E,F在对角线BD上,且BE=DF,求证: 
(1)AE=CF;
(2)四边形AECF是平行四边形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
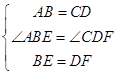 ,
,
∴△ABE≌△DCF(SAS).
∴AE=CF.
(2)证明:∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
【解析】(1)根据平行四边形的性质可得AB=CD,AB∥CD,然后可证明∠ABE=∠CDF,再利用SAS来判定△ABE≌△DCF,从而得出AE=CF.(2)首先根据全等三角形的性质可得∠AEB=∠CFD,根据等角的补角相等可得∠AEF=∠CFE,然后证明AE∥CF,从而可得四边形AECF是平行四边形.
【考点精析】关于本题考查的平行四边形的判定与性质,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若10个数据x1,x2,x3,…,x10的方差为3,则数据x1+1,x2+1,x3+1,…,x10+1的方差为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解九年级上学期期末考试数学成绩,从九年级学生中随机抽取了部分学生进行调查,并将所抽取的学生数学成绩(成绩均为整数)分为A、B、C、D、E五个等级,A:50.5~60.5,B:60.5~70.5,C:70.5~80.5,D:80.5~90.5,E:90.5~100.5,并绘制了如图所示的频数分布直方图和扇形统计图,请你根据统计图提供的信息解答下列问题:

(1)这次抽样调查共抽取了多少名学生?
(2)请把频数分布直方图补充完整;
(3)这次期末考试数学成绩的中位数落在哪个等级内?
(4)该校九年级有800名学生,若规定80分以上(不含80分)为良好,试估计九年级有多少名学生的数学成绩为良好? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度,可量出约为__________cm;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】650万用科学记数法表示应是( )
A.0.65×107
B.6.5×106
C.65×105
D.65×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 (a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
A. 2a﹣b=0
B. a+b+c>0
C. 3a﹣c=0
D. 当a=
 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形 -
科目: 来源: 题型:
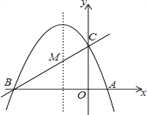
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
相关试题

