【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC. 
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE=时,四边形BFCE是菱形.
参考答案:
【答案】
(1)证明:∵AB=DC,
∴AC=DB,
在△AEC和△DFB中
 ,
,
∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF
∴EC∥BF,
∴四边形BFCE是平行四边形
(2)4
【解析】(2)当四边形BFCE是菱形时,BE=CE,
∵AD=10,DC=3,AB=CD=3,
∴BC=10﹣3﹣3=4,
∵∠EBD=60°,
∴BE=BC=4,
∴当BE=4 时,四边形BFCE是菱形,
故答案为:4.
(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠,分别在BC、AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG=
 ,A′G=6,C′G=1,则矩形纸片ABCD的周长为 .
,A′G=6,C′G=1,则矩形纸片ABCD的周长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,A,B,C三点都在小方格的顶点上(每个小方格的边长为1).

(1)在图甲中画一个以A,B,C为其中三个顶点的平行四边形,并求出它的周长.
(2)在图乙中画一个经过A,B,C三点的圆,并求出圆的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋里装有2个红球,1个白球,1个黄球,它们除颜色外其余都相同.
(1)求从袋中摸出一个球是黄球的概率.
(2)摸出一个球,记下颜色后不放回,搅拌均匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表). -
科目: 来源: 题型:
查看答案和解析>>【题目】某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销,经过调查,得到如下数据:

销售单价x(元/件)
…
20
30
40
50
60
…
每天销售量y(件)
…
500
400
300
200
100
…
(1)把上表中x,y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式.
(2)当销售单价为多少元时,工艺品厂试销该小工艺品每天获得的利润最大?最大利润是多少?(利润=销售额﹣成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
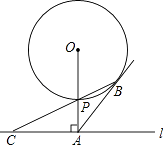
(1)求证:AB=AC.
(2)若PC=2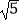 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.

(1)求抛物线的函数表达式.
(2)判断△ADC的形状,并说明理由.
(3)对称轴DE上是否存在点P,使点P到直线AD的距离与到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由.
相关试题

