Question

【题目】如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP，DQ．

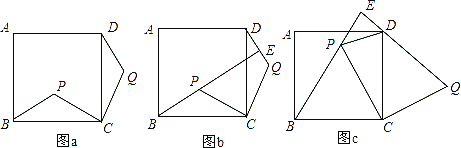
(1)、如图a，求证：△BCP≌△DCQ；

(2)、如图，延长BP交直线DQ于点E．

①如图b，求证：BE⊥DQ；

②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．

Answer 1

【答案】（1）证明见试题解析；（2）①证明见试题解析；②△DEP为等腰直角三角形．

【解析】试题分析：(1)、根据正方形性质得出BC=DC，根据旋转图形的性质得出CP=CQ以及∠PCB=∠QCD，从而得出三角形全等；(2)、①、根据全等得出∠PBC＝∠QBC，设BE和CD交点为M，根据对顶角得出∠DME=∠BMC，从而说明BE⊥QD；②、根据等边三角形的性质得出PB=PC=BC，∠PBC=∠BPC=∠PCB=60°，则∠PCD=30°，根据BC=DC，CP=CQ得出△PCD为等腰三角形，然后根据△DCQ为等边三角形，从而得出∠DEP=90°，从而得出答案.

试题解析：(1)、∵四边形ABCD是正方形，∴BC＝DC

又∵将线段CP绕点C顺时针旋90°得到线段CQ，∴CP=CQ,∠PCQ＝90°∴∠PCD+∠QCD＝90°

又∵∠PCB+∠PCD=90° ∴∠PCB=∠QCD

在△BCP和△DCQ中 BC=DC，CP=CQ，∠PCB=∠QCD ∴△BCP≌△DCQ

(2)、①∵△BCP≌△DCQ ∴∠PBC＝∠QBC

设BE和CD交点为M ∴∠DME=∠BMC ∠MED=∠MCB=90°∴BE⊥QD

②△DEP为等腰直角三角形，

∵△BOP为等边三角形 ∴PB=PC=BC ∠PBC=∠BPC=∠PCB=60°

∴∠PCD=90°-60°=30°∴∠DCQ=90°-60°=30°

又∵BC＝DC CP=CQ∴PC＝DC DC＝CQ ∴△PCD是等腰三角形

△DCQ是等边三角形 ∴∠CPD＝∠CDP＝75°∠CDQ＝60°∴∠EPD=180°-15°-60°=45°

∠EDP=180°-75°-60°="45" °∴∠EPD=∠EDP PE=DE ∴∠DEP=180°-45°-45°=90°

∴△DEP是等腰直角三形