【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
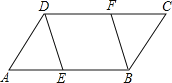
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF;
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行四边形,又DF=FB,可根据邻边相等的平行四边形为菱形证出结论.
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
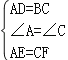 ,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是( )
A.Q=8x
B.Q=8x﹣50
C.Q=50﹣8x
D.Q=8x+50 -
科目: 来源: 题型:
查看答案和解析>>【题目】若y=x+2﹣b是正比例函数,则b的值是( )
A.0
B.﹣2
C.2
D.﹣0.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】去年某省将地处A,B两地的两所大学合并成了一所综合性大学,为了方便A,B两地师生的交往,学校准备在相距(1+
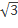 )km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东600方向、B地的西偏北450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
)km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东600方向、B地的西偏北450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?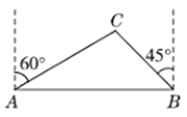
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.

(1)、求点A、B的坐标;
(2)、已知点C(-2,2),求△BOC的面积;
(3)、点P是第一象限角平分线上一点,若
 ,求点P的坐标.
,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,F为DC的中点,E为BC 上一点,BC=4CE.求证:AF⊥FE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.
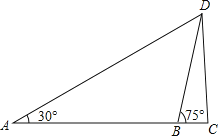
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
相关试题

