【题目】如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.
(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
参考答案:
【答案】
(1)
解:
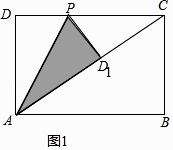
如图1,∵由题意得:△ADP≌△AD1P,
∴AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,
∵直线AD1过C,
∴PD1⊥AC,
在Rt△ABC中,AC= ![]() =
= ![]() ,CD1=
,CD1= ![]() ﹣2,
﹣2,
在Rt△PCD1中,PC2=PD12+CD12,
即(3﹣x)2=x2+( ![]() ﹣2)2,
﹣2)2,
解得:x= ![]() ,
,
∴当x= ![]() 时,直线AD1过点C
时,直线AD1过点C
(2)
解:如图2,

连接PE,
∵E为BC的中点,
∴BE=CE=1,
在Rt△ABE中,AE= ![]() =
= ![]() ,
,
∵AD1=AD=2,PD=PD1=x,
∴D1E= ![]() ﹣2,PC=3﹣x,
﹣2,PC=3﹣x,
在Rt△PD1E和Rt△PCE中,
x2+( ![]() ﹣2)2=(3﹣x)2+12,
﹣2)2=(3﹣x)2+12,
解得:x= ![]() ,
,
∴当x= ![]() 时,直线AD1过BC的中点E;
时,直线AD1过BC的中点E;
(3)
解:如图3,
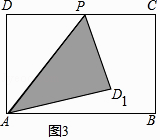
当0<x≤2时,y=x,
如图4,
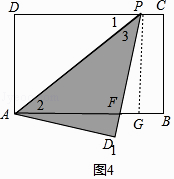
当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,
∵AB∥CD,
∴∠1=∠2,
∵∠1=∠3(根据折叠),
∴∠2=∠3,
∴AF=PF,
作PG⊥AB于G,
设PF=AF=a,
由题意得:AG=DP=x,FG=x﹣a,
在Rt△PFG中,由勾股定理得:(x﹣a)2+22=a2,
解得:a= ![]() ,
,
所以y= ![]() =
= ![]() ,
,
综合上述,当0<x≤2时,y=x;当2<x≤3时,y= ![]()
【解析】(1)根据折叠得出AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,在Rt△ABC中,根据勾股定理求出AC,在Rt△PCD1中,根据勾股定理得出方程,求出即可;(2)连接PE,求出BE=CE=1,在Rt△ABE中,根据勾股定理求出AE,求出AD1=AD=2,PD=PD1=x,D1E= ![]() ﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;(3)分为两种情况:当0<x≤2时,y=x;当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,求出AF=PF,作PG⊥AB于G,设PF=AF=a,在Rt△PFG中,由勾股定理得出方程(x﹣a)2+22=a2 , 求出a即可.
﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;(3)分为两种情况:当0<x≤2时,y=x;当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,求出AF=PF,作PG⊥AB于G,设PF=AF=a,在Rt△PFG中,由勾股定理得出方程(x﹣a)2+22=a2 , 求出a即可.
【考点精析】掌握全等三角形的性质和勾股定理的概念是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017威海)央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:

(1)此次共调查了名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:
如图2,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10cm,DE=120cm,FG⊥DE,垂足为点G.
(参考数据:sin37°50′≈0.61,cos37°50′≈0.79,tan37°50′≈0.78)
(1)若∠θ=37°50′,则AB的长约为cm;
(2)若FG=30cm,∠θ=60°,求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.
(1)如图1,若DE∥AB,求证:CF=EF;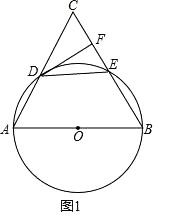
(2)如图2,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3)点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.
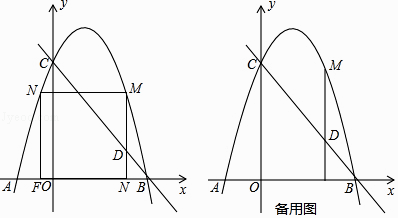
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3)若∠DMN=90°,MD=MN,求点M的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b(k≠0)的图象经过A(﹣1,﹣4),B(2,2)两点,P为反比例函数y=
 图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )
图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )
A.2
B.4
C.8
D.不确定
相关试题

