搜索
【题目】如图，将一条长为60cm的卷尺铺平后沿着图中箭头的方向折叠，使得卷尺自身的一部分重合，然后在重合部分沿与卷尺的边垂直的方向剪一刀，此时卷尺分为了三段，若这三段长度比为1：2：3，则折痕对应的刻度可能的值有 ________．
参考答案：
【答案】20，25，35，40
【解析】试题解析：∵三段长度由短到长的比为1：2：3，
∴三段长度分别为：10cm，20cm，30cm．
①当剪切处右边上部分的长度为10cm，剪切处左边的卷尺为20cm时，
折痕处为：10+
=20cm；
②当剪切处右边上部分的长度为10cm，剪切处左边的卷尺为30cm时，
折痕处为：10+
=25cm；
③当剪切处右边上部分的长度为20cm，剪切处左边的卷尺为10cm时，
折痕处为：20+
=25cm；
④当剪切处右边上部分的长度为20cm，剪切处左边的卷尺为30cm时，
折痕处为：20+
=35cm；
⑤当剪切处右边上部分的长度为30cm，剪切处左边的卷尺为10cm时，
折痕处为：30+
=35cm；
⑥当剪切处右边上部分的长度为30cm，剪切处左边的卷尺为20cm时，
折痕处为：30+
=40cm；
综上所述，折痕对应的刻度有4种可能：20cm，25cm，35cm，40cm.
故答案为：20cm，25cm，35cm，40cm.
-
科目： 来源： 题型：
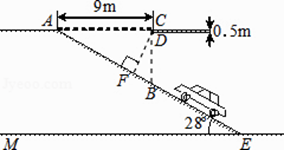
查看答案和解析>>【题目】随着人们经济收入的不断提高，汽车已越来越多地进入到各个家庭．某大型超市为缓解停车难问题，建筑设计师提供了楼顶停车场的设计示意图．按规定，停车场坡道口上坡要张贴限高标志，以便告知车辆能否安全驶入．如图，地面所在的直线ME与楼顶所在的直线AC是平行的，CD的厚度为0.5m，求出汽车通过坡道口的限高DF的长（结果精确到0.1m，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，对角线AC与BD相交于O，不能判定四边形ABCD是平行四边形的是（ ）
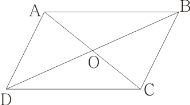
A. AB∥CD,AO=CO B. AB∥DC,∠ABC=∠ADC
C. AB=DC,AD=BC D. AB=DC,∠ABC=∠ADC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P是矩形ABCD的AD边上一个动点，矩形的两条边AB、BC长分别是6和8，则点P到矩形的两条对角线距离之和PE+PF是（ ）
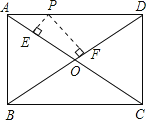
A. 4.8 B. 5 C. 6 D. 7.2
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小丁在研究数学问题时遇到一个定义：对于排好顺序的三个数：
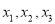，称为数列
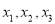.计算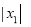
， 
， 
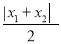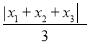将这三个数的最小值称为数列
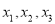的价值．例如，对于数列2，﹣1，3，因为
， 
， 
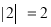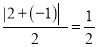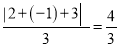，所以数列2，﹣1，3的价值为
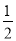．小丁进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的价值．如数列﹣1，2，3的价值为
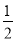；数列3，﹣1，2的价值为1；…．经过研究，小丁发现，对于“2，﹣1，3”这三个数，按照不同的排列顺序得到的不同数列中，价值的最小值为
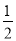．根据以上材料，回答下列问题：（1）数列﹣4，﹣3，2的价值为 ；
（2）将“﹣4，﹣3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的价值的最小值为 ，取得价值最小值的数列为 （写出一个即可）；
（3）将2，﹣9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的价值的最小值为1，则a的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是（A，B）的好点．
（1）如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D______（A，B）的好点，但点D______（B，A）的好点．（请在横线上填是或不是）知识运用：
（2）如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为-2．数______所表示的点是（M，N）的好点；
（3）如图3，A、B为数轴上两点，点A所表示的数为-20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当经过______秒时，P、A和B中恰有一个点为其余两点的好点？
-
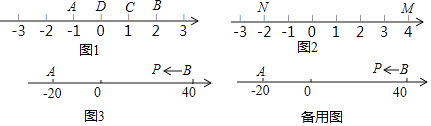
科目： 来源： 题型：
查看答案和解析>>【题目】某月份的日历表如图．任意圈出一横行或一竖列相邻的三个数．这三个数的和不可能是（ ）
A. 24 B. 42 C. 58 D. 66
相关试题
