【题目】随着经济的发展,能源与环境已成为人们日益关注的问题.据统计,全球每年大约会产生近3亿吨的塑料垃圾(例如平时用的矿泉水瓶子等)和约5亿吨的废钢铁(例如平时扔掉的易拉罐等),某中学为了培养学生的环保意识,开展了“环境保护,从我做起”的主题活动,七(2)班同学在活动中积极响应,在甲小区设立了回收塑料瓶和易拉罐的两个垃圾桶,班长小明对2周的收集情况进行了统计,根据下列统计表和废品收购站的价格表,解决下列问题:


(1)全班2周共收集了 斤塑料瓶,收集了 斤易拉罐.
(2)班委会决定给贫困山区的孩子们捐赠一套价值50.4元的励志丛书,你认为按照这样的收集速度,至少需要收集几周才能实现这个愿望?写出计算过程.
(3)七(1)班在乙小区也设立了塑料瓶和易拉罐的回收点,两周收集塑料瓶和易拉罐共计440个,按相同价格出售后,所得金额比七(2)班两个周的废品回收金额多1.8元,求七(1)班同学两周收集的塑料瓶和易拉罐各多少个?
参考答案:
【答案】(1)5,7.2,(2)需要收集6个周才能实现这个愿望,(3)七(1)班同学两周收集的塑料瓶320个和易拉罐120个.
【解析】
由图标可知,两周分别收集塑料瓶和易拉罐的个数=第一周个数+第二周的个数;由塑料瓶和易拉罐一斤的个数,进而分别求出塑料瓶和易拉罐的斤数=总个数÷一斤的个数
由(1)知,每两周收集的斤数,可得出两周挣的钱数,进而求出一周挣的钱数,再用书的钱数÷一周的钱数即为所求
设七(1)班同学两周收集的塑料瓶x个和易拉罐(440﹣x)个,根据七(1)班同学两周收集的塑料瓶钱数+易拉罐钱数=七(2)班同学两周收集的总钱数+1.8,的等量关系列出方程求解即可
解:(1)由图表可知:
96+104=200(个),
全班2个周收集了塑料瓶200个,
200÷40=5(斤),
即全班2个周收集了5斤塑料瓶,
64+80=144(个),
全班2个周收集了易拉罐144个,
144÷20=7.2(斤),
即全班2个周收集了7.2斤易拉罐,
故答案为:5,7.2,
(2)由(1)可知:全班每2周收集塑料瓶5斤,易拉罐7.2斤,
1.2×5+1.5×7.2=16.8(元),
即每2周全班可通过卖废品挣16.8元,
16.8÷2=8.4(元),
即平均每周全班可通过卖废品挣8.4元,
50.4÷8.4=6(周),
即需要收集6个周才能实现这个愿望,
(3)设七(1)班同学两周收集的塑料瓶x个和易拉罐(440﹣x)个,
1.2×![]() +1.5×
+1.5×![]() =16.8+1.8,
=16.8+1.8,
解得:x=320,
440﹣320=120(个),
答:七(1)班同学两周收集的塑料瓶320个和易拉罐120个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
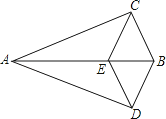
(1)∠CEB=∠CBE;
(2)四边形BCED是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
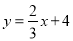 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0) B.(﹣6,0) C.(
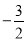 ,0) D.(
,0) D.(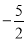 ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价和零售价(单位:元/kg)如下表所示:
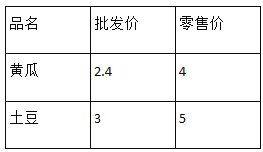
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装部分为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额的数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
该商场服装营业员的人数为 ,图①中m的值为 ;
求统计的这组销售额数据的平均数、众数和中位数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%
根据图表中提供的信息,解答下列问题:
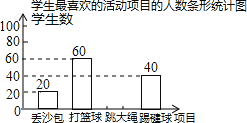
(1)m= , n= , p=;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

相关试题

