搜索
【题目】如图，△ABC的面积为
．第一次操作：分别延长
，
，
至点
，
，
，使
，
，
，顺次连接，，，得到△
．第二次操作：分别延长
，
，
至点
，
，
，使
，
，
，顺次连接，，，得到△
，…按此规律，要使得到的三角形的面积超过2020，最少经过多少次操作（ ）
A.
B.
C.
D.
参考答案：
【答案】A
【解析】
先根据已知条件求出△A1B1C1及△A2B2C2的面积，再根据两三角形的倍数关系求解即可．
解：连接A1C，如图，
∵AB＝A1B，
∴△ABC与△A1BC的面积相等，
∵△ABC面积为1，
∴
＝1．
∵BB1＝2BC，
∴
＝2，
同理可得，
＝2，
＝2，
∴
＝2+2+2+1＝7；
同理可得：△A2B2C2的面积＝7×△A1B1C1的面积＝49，
第三次操作后的面积为7×49＝343，
第四次操作后的面积为7×343＝2401．
故按此规律，要使得到的三角形的面积超过2020，最少经过4次操作．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】五一小长假的某一天，亮亮全家上午
时自驾小汽车从家里出发，到某旅游景点游玩，该小汽车离家的距离（千米）与时间（时）之间的关系如图所示，根据图像提供的有关信息，判断下列说法错误的是（ ）
A.景点离亮亮的家
千米B.亮亮到家的时间为
时C.小汽车返程的速度为
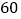千米/时D.
时至
时，小汽车匀速行驶 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，∠B=30°，将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角最小为（ ）
A.115°
B.125°
C.120°
D.145° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，∠APD=30°，则∠ADP的度数为（ ）
A.45°
B.40°
C.35°
D.30° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=mx+n与正比例函数y=mnx（m，n为常数，且mn≠0，n＞0）的图象是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，AD＝5，BC＝18，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动，当运动时间t秒时，以点P，Q，E，D为顶点的四边形是平行四边形，则t的值为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，D是AB上一动点，过点D作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是（ ）
A.5
B.4.8
C.4.6
D.4.4
相关试题
