【题目】如图1,以直角三角形的各边边边分别向外作正三角形,再把较小的两张正三角形纸片按图2的方式放置在最大正三角形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积B.较小两个正三角形重叠部分的面积
C.最大正三角形的面积D.最大正三角形与直角三角形的面积差
参考答案:
【答案】B
【解析】
根据勾股定理得到c2=a2+b2,根据正方形的面积公式、长方形的面积公式计算即可.
设直角三角形的斜边长为c,较长直角边为b,较短直角边为a,
由勾股定理得,c2=a2+b2
阴影部分的面积=c2-b2-a(c-b)=a2-ac+ab=a(a+b-c)
较小两个正方形重叠部分的长=a(c-b),宽=a,
则较小两个正方形重叠部分底面积=a(a+b-c),
∴知道图中阴影部分的面积,则一定能求出
较小两个正方形重叠部分的面积,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45
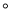 ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.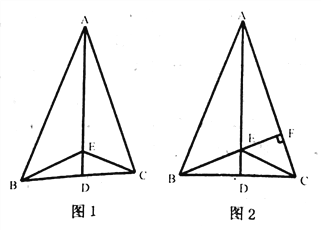
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
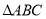 中,
中, ,
,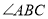 与
与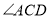 的平分线交于点
的平分线交于点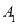 ,得
,得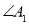 ;
;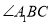 与
与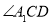 的平分线相交于点
的平分线相交于点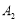 ,得
,得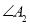 ;……;
;……;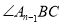 与
与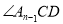 的平分线交于点
的平分线交于点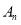 ,要使
,要使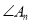 的度数为整数,则
的度数为整数,则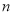 的最大值为( )
的最大值为( )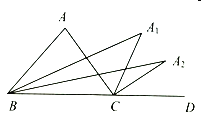
A.4B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过
A. 第一、二、三、四象限 B. 第一、二、三象限
C. 第一、二、四象限 D. 第二、三、四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
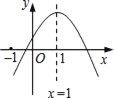
A. ①③ B. ②③ C. ①④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一块等腰直角三角板
 放置在平面直角坐标系中,
放置在平面直角坐标系中,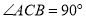 ,
,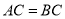 ,点
,点 在
在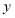 轴的正半轴上,点
轴的正半轴上,点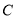 在
在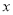 轴的负半轴上,点
轴的负半轴上,点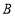 在第二象限,
在第二象限,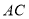 所在直线的函数表达式是
所在直线的函数表达式是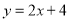 ,若保持
,若保持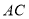 的长不变,当点
的长不变,当点 在
在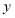 轴的正半轴滑动,点
轴的正半轴滑动,点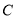 随之在
随之在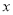 轴的负半轴上滑动,则在滑动过程中,点
轴的负半轴上滑动,则在滑动过程中,点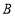 与原点
与原点 的最大距离是__________.
的最大距离是__________.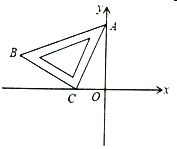
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
相关试题

