【题目】对于二次函数y=﹣(x﹣1)2+2的图象与性质,下列说法正确的是( )
A.对称轴是直线x=1,最小值是2
B.对称轴是直线x=1,最大值是2
C.对称轴是直线x=﹣1,最小值是2
D.对称轴是直线x=﹣1,最大值是2
参考答案:
【答案】B
【解析】解:由抛物线的解析式:y=﹣(x﹣1)2+2,
可知:对称轴x=1,
开口方向向下,所以有最大值y=2,
所以答案是:B
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个数的和是10,其中一个数用字母x表示,那么表示这两个数的积的代数式是( )
A. 10x B. x (10+x) C. x (10-x) D. x (x-10)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次英语测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据说法正确的是( )
A.中位数是91 B.平均数是91 C.众数是91 D.极差是78
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
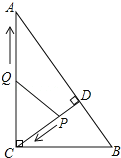
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数中:﹣8,2.7,0.66666…,0,2,9.181181118…是无理数的有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3(x﹣4)2+5的顶点坐标为( )
A.(﹣4,﹣5)
B.(﹣4,5)
C.(4,﹣5)
D.(4,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】据报载,2014年我国发展固定宽带接入新用户25000000户,其中25000000用科学记数法表示为_______.
相关试题

