【题目】如图,直线l:![]() 与
与![]() 轴交于点A,将直线l绕点A顺时针旋转75后,所得直线的解析式为( )
轴交于点A,将直线l绕点A顺时针旋转75后,所得直线的解析式为( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
如下图,AC为直线l绕点A顺时针旋转75°所得直线,由已知条件易得OB=1,OA=![]() ,从而可得AB=2,结合∠AOB=90°可得∠BAO=30°,由题意可知∠BAC=75°,从而可得∠OAC=45°,由此可得OC=OA=
,从而可得AB=2,结合∠AOB=90°可得∠BAO=30°,由题意可知∠BAC=75°,从而可得∠OAC=45°,由此可得OC=OA=![]() ,从而可得点C的坐标,这样结合点A的坐标即可求得直线AC的解析式了.
,从而可得点C的坐标,这样结合点A的坐标即可求得直线AC的解析式了.
如下图,设直线AC是直线l绕点A旋转75°后所得直线:
∵在直线l:![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴点A的坐标为![]() ,点B的坐标为(1,0),
,点B的坐标为(1,0),
∴OA=![]() ,OB=1,
,OB=1,
∵∠AOB=90°,
∴AB=2=2OB,
∴∠BAO=30°,
∵由题意可知∠BAC=75°,
∴∠OAC=45°,
∴△AOC是等腰直角三角形,
∴OC=OA=![]() ,
,
∴点C的坐标为![]() ,
,
设直线AC的解析式为:![]() ,
,
则:![]() ,解得
,解得![]() ,
,
∴AC的解析式为:![]() .
.
故选B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
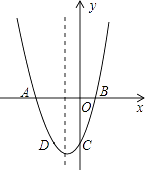
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
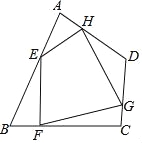
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为1,把它放在如图所示的直角坐标系中,点M(t,0)是x轴上一个动点(t≥1),连接BM,在BM的右侧作正方形BMNP;直线DE的解析式为y=2x+b,与x轴交于点D,与y轴交于点E,当△PDE为等腰直角三角形时,点P的坐标是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕点B顺时针旋转到平行四边形A1BC1D1的位置,此时C1D1恰好经过点C,则∠ABA1=______°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(k﹣1)x2﹣
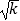 x+
x+  =0有实数根,则k的取值范围是( )
=0有实数根,则k的取值范围是( )
A.k为任意实数
B.k≠1
C.k≥0
D.k≥0且k≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费=自来水销售费用+污水处理费用)
自来水销售价格
污水处理价格
每户每月用水量
单价:元/吨
单价:元/吨
17吨及以下
a
0.80
超过17吨不超过30吨的部分
b
0.80
超过30吨的部分
6.00
0.80
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a,b的值.
(2)小王家6月份交水费184元,则小王家6月份用水多少吨?
相关试题

