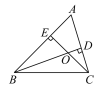
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
参考答案:
【答案】=180
【解析】
根据三角形内角和等于180°,四边形内角和等于360°可求解.
∵BD是AC边上的高,CE是AB边上的高,
∴∠AEC=∠ADB=90°
∵∠ABD+∠A+∠ADB=180°,∠ACE+∠A+∠AEC=180°,
∴∠ABD=180°-∠A-∠ADB,∠ACE=180°-∠A-∠AEC,
∴∠ABD=∠ACE,
在四边形AEOD中,∵∠A+∠AEO+∠EOD+∠ODA=360°,
∵∠AEC=∠ADB=90°,
∴∠A+∠EOD=360°-∠AEO-∠ODA=360°-90°-90°=180°.
故答案为:=;180.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣6,0)、B(﹣2,3)、
C(﹣1,0).
(1)请直接写出与点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
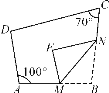
A. 115° B. 105° C. 95° D. 85°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少? -
科目: 来源: 题型:
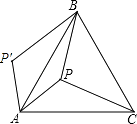
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.
-
科目: 来源: 题型:
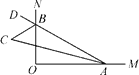
查看答案和解析>>【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
相关试题

