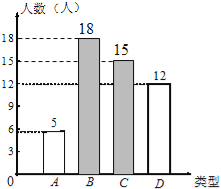
【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图:

请你根据图中提供的信息完成下列各题:
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)观察统计图,先用A类的人数除以它所占的百分比得到总人数,再利用扇形统计图计算出C类人数,接着计算出D类人数,然后补全条形统计图;
(2)通过列表法展示所有12种等可能情况,再找出1人主持过班会而另一人没主持过班会的结果数,然后根据概率公式求解.
解:(1)调查的学生总数为5÷10%=50(人),
C类人数为50×![]() =15(人),
=15(人),
D类人数为50﹣5﹣15﹣12=18(人),
条形统计图为:
(2)设主持过班会的两人分别为A1、A2,另两人分别为B1、B2,填表如下:
结果 第二人
第一人 A1A2B1B2
A1(A1,A2) (A1,B1) (A1,B2)
A2(A2,A1) (A2,B1) (A2,B2)
B1(B1,A1) (B1,A2) (B1,B2)
B2(B2,A1) (B2,A2) (B2,B1)
由列表可知,共有12种等可能情况,其中有8种符合题意,
所以P(抽出1人主持过班会而另一人没主持过班会)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在给定的条件中,能画出平行四边形的是( )
A. 以60cm为一条对角线,20cm,34cm为两条邻边
B. 以6cm,10cm为两条对角线,8cm为一边
C. 以20cm,36cm为两条对角线,22cm为一边
D. 以6cm为一条对角线,3cm,10cm为两条邻边
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(2﹣π)0+( )﹣2+(﹣2)3
)﹣2+(﹣2)3
(2)0.5200×(﹣2)202
(3)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(4)(3x﹣1)(x+1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本中的50个数据分别落在五个小组内,第一、三、四、五组数据的个数分别为2,8,10,20,则第二小组的频数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于x的单项式,探究其规律:2x,4x2 , 6x3 , 8x4 , 10x5 , 12x6 , …,按照上述规律,第2016个单项式是( )
A.2016x2015
B.2016x2016
C.4032x2015
D.4032x2016 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)如图1,若E为AB的中点,请直接写出F、D两点的坐标:F( , ) D( , )
(2)如图1,连接CD,在(1)的条件下,求证:CD=FD.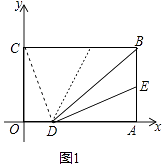
(3)如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.
相关试题

