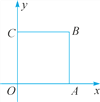
【题目】如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
(1)点A的坐标为______,点C的坐标为_______.
(2)判断直线y=-2x+![]() 与正方形OABC是否有交点,并说明理由.
与正方形OABC是否有交点,并说明理由.
(3)将直线y=-2x+![]() 进行平移,恰好能把正方形OABC分成面积相等的两部分,请求出平移后的直线的函数表达式.
进行平移,恰好能把正方形OABC分成面积相等的两部分,请求出平移后的直线的函数表达式.
参考答案:
【答案】(1)(1,0),(0,1);(2)有,理由见解析;(3)y=-2x+![]()
【解析】试题分析:(1)利用正方形的性质,可得A,C的坐标. (2)求出y=-2x+![]() 与坐标轴的交点,易得结论.(3)要想平分正方形的面积,直线必须通过正方形的中心,所以求出正方形的中心坐标,代入平移的直线方程可得所求.
与坐标轴的交点,易得结论.(3)要想平分正方形的面积,直线必须通过正方形的中心,所以求出正方形的中心坐标,代入平移的直线方程可得所求.
试题解析:(1)利用正方形的性质,可得A(1,0),C(0,1).
(2)有.理由如下:
把x=0代入y=-2x+![]() ,得y=
,得y=![]() ;
;
把y=0代入y=-2x+![]() ,得-2x+
,得-2x+![]() =0,解得x=
=0,解得x=![]() .
.
∴直线y=-2x+![]() 与坐标轴的交点为
与坐标轴的交点为![]() 和
和![]() .
.
∵OC=1,OA=1,∴直线与正方形有交点.
(3)设平移后的直线的函数表达式为y=-2x+b.
根据题意,易得直线y=-2x+b应经过AC与BO的交点,即过正方形OABC的中心点![]() .
.
把点![]() 的坐标代入y=-2x+b,得-2×
的坐标代入y=-2x+b,得-2×![]() +b=
+b=![]() ,解得b=
,解得b=![]() .
.
∴所求直线的函数表达式为y=-2x+![]() .
.
-
科目: 来源: 题型:
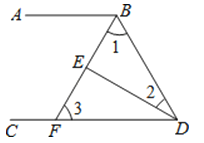
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.猜想∠2与∠3的关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(5,y)与点N(x、-6)关于x轴对称,则x、y的值分别为( )
A. 5,-6 B. 5,6 C. -5,-6 D. -5,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 一次函数的图象与x轴,y轴分别相交于点A,B,将△AOB沿直线AB翻折,得△ACB.若点C
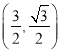 ,求该一次函数的表达式.
,求该一次函数的表达式.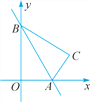
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①、②,解答下面各题:
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数.
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)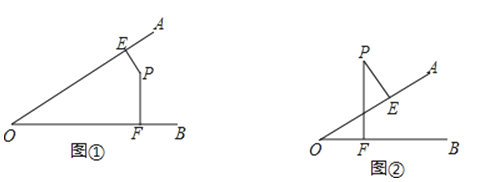
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?若设应安排x名工人生产螺钉,则生产螺母的有_____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知正比例函数
 与一次函数
与一次函数 的图像交于点A.
的图像交于点A.(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交
 和
和 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC= OA,求△OBC的面积.
OA,求△OBC的面积.
相关试题

