【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
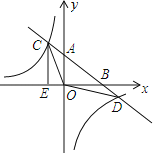
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积;
(3)直接写出使一次函数值小于反比例函数值的x的取值范围.
参考答案:
【答案】(1)y=﹣![]() x+2.y=﹣
x+2.y=﹣![]() .(2)8;(3)﹣2<x<0或x>6.
.(2)8;(3)﹣2<x<0或x>6.
【解析】
试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解;
(3)根据函数的图象和交点坐标即可求得.
解:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=![]() =
=![]() =
=![]() .
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(﹣2,3).
设直线AB的解析式为y=kx+b,则![]() ,
,
解得 .
.
故直线AB的解析式为y=﹣![]() x+2.
x+2.
设反比例函数的解析式为y=![]() (m≠0),
(m≠0),
将点C的坐标代入,得3=![]() ,
,
∴m=﹣6.
∴该反比例函数的解析式为y=﹣![]() .
.
(2)联立反比例函数的解析式和直线AB的解析式可得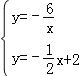 ,
,
可得交点D的坐标为(6,﹣1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8;
(3)由图象得,一次函数值小于反比例函数值的x的取值范围:﹣2<x<0或x>6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2,4,4,4,6的众数是 ,平均数是 .
-
科目: 来源: 题型:
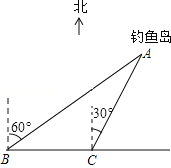
查看答案和解析>>【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行 海里与钓鱼岛A的距离最近?
-
科目: 来源: 题型:
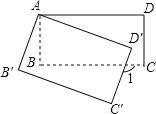
查看答案和解析>>【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=100,∠B=3∠C,则∠B=__________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2y﹣4y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC=BD时,它是正方形
C.当AC⊥BD时,它是菱形
D.当∠ABC=90°时,它是矩形
相关试题

