【题目】新冠肺炎使得湖北的物资紧缺,为支援疫区,某村捐赠蔬菜30吨,水果13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量(单位:吨)是其可装的水果重量的4倍,一辆乙种货车可装蔬菜水果各2吨;
(1)一辆甲种货车可装载蔬菜、水果各多少吨?
(2)该村安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1500元,则该村应选择哪种方案?使运费最少?最少运费是多少元?
参考答案:
【答案】(1)4;1 (2)三种方案:甲5辆,乙5辆;甲6辆,乙4辆;甲7辆,乙3辆 (3)方案1;17500元
【解析】
(1)设一辆甲种货车可装载蔬菜x吨,水果y吨,根据“一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量是其可装的水果重量的4倍”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设安排m辆甲种货车,则安排(10-m)辆乙种货车,根据这10辆车可一次将30吨蔬菜和13吨水果运完,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数,即可得出各运货方案;
(3)根据总运费=单辆车的运费×所用该种车型的辆数,即可分别求出三种运货方案所需总运费,比较后即可得出结论.
解:(1)设一辆甲种货车可装载蔬菜x吨,水果y吨, 依题意,得:
![]() ,
,
解得:![]() .
.
答:一辆甲种货车可装载蔬菜4吨,水果1吨.
(2)设安排m辆甲种货车,则安排(10-m)辆乙种货车, 依题意,得:
![]()
解得:5≤m≤7.
∵m为整数,
∴m=5,6,7,
∴共有三种方案,
方案1:安排5辆甲种货车,5辆乙种货车;
方案2:安排6辆甲种货车,4辆乙种货车;
方案3:安排7辆甲种货车,3辆乙种货车.
(3)方案1所需费用2000×5+1500×5=17500(元);
方案2所需费用2000×6+1500×4=18000(元);
方案3所需费用2000×7+1500×3=18500(元).
∵17500<18000<18500,
∴该果农应选方案1,使运费最少,最少运费是17500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有________.(填上所有正确结论的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若
 ,则下列式子中错误的是( )
,则下列式子中错误的是( )A.
 B.
B. 
C.
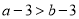 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )
A.
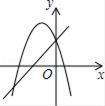 B.
B. 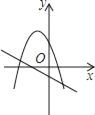 C.
C. 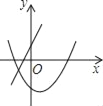 D.
D. 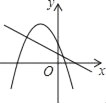
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴交于点A,与y轴交于点B,与直线
与x轴交于点A,与y轴交于点B,与直线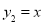 交于点E,点E的横坐标为3.
交于点E,点E的横坐标为3.(1)直接写出b值:___;
(2)在y轴上有一点M,使得△ABM是等腰三角形,直接写出所有可能的点M的坐标: ;
(3)在x轴上有一点P(m,0),过点P作x轴的垂线,与直线
 交于点C,与直线
交于点C,与直线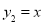 交于点D,若CD=2OB,求m的值.
交于点D,若CD=2OB,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为
 .
.(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学习随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次共抽取了 名学生进行调查统计,扇形统计图中D类所对应的扇形圆心角大小为 ;
(2)将条形统计图补充完整;
(3)如果该校共有2000名学生,请你估计该校C类学生约有多少人?
相关试题

