【题目】如图,点C在线段AB上,且AC︰BC=5︰2,点D是线段BC的中点,点E是线段AD的中点,AB=14,求线段CE的长.
![]()
参考答案:
【答案】CE=2
【解析】试题分析:首先根据AC︰BC=5︰2, AB=14求出AC,BC的长, 再根据点D是线段BC的中点求出CD的长,进而求出AD的长, 最后根据点E是线段AD的中点求出AE的长,即可求出CE的长.
试题解析:
设AC=5x,BC=2x.
则5x+2x=14
解得:x=2
故:AC=10,BC=4
点D是线段BC的中点,CD=![]() BC=2
BC=2
故AD=16
点E是线段AD的中点,AE=AD=8
∴CE=AC-AE=10-8=2
点睛: 本题考查了线段中点的定义和求两点之间的距离的应用,主要考查学生的理解能力和计算能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(a+2b)(2a﹣4b)=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列表述中,不能表示代数式“4a”的意义的是( )
A.4的a倍
B.a的4倍
C.4个a相加
D.4个a相乘 -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60°
B.45°,45°
C.45°,90°
D.20°,70° -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)5x2+10x+5
(2)(a+4)(a﹣4)+3(a+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】人和人之间讲友情,有趣的是,数与数之间也有相类似的关系. 若两个不同的自然数的所有真因数(即除了自身以外的正约数)之和相等,我们称这两个数为“亲和数”. 例如:18的约数有1、2、3、6、9、18,它的真因数之和1+2+3+6+9=21;51的约数有1、3、17、51,它的真因数之和1+3+17=21,所以18和51为“亲和数”. 数还可以与动物形象地联系起来,我们称一个两头(首位与末位)都是
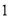 的数为“两头蛇数”.
的数为“两头蛇数”.(1)6的“亲和数”为 ;将一个四位的“两头蛇数”去掉两头,得到一个两位数,它恰好是这个“两头蛇数”的约数,求满足条件的“两头蛇数”.
(2)已知两个“亲和数”的真因数之和都等于15,且这两个“亲和数”中较大的数能将一个正中间数位(百位)上的数为4的五位“两头蛇数”整除,若这个五位“两头蛇数”的千位上的数字小于十位上的数字,求满足条件的“两头蛇数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是随机事件的是( )
A.2019年1月有31天
B.2019年4月7日丰都庙会开幕式当天天气晴朗
C.踢飞在空中的足球会下落
D.早上的太阳从东方升起
相关试题

