【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有个.

A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
【解析】∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
AE=AF,AB=AD,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°(故②正确),
∵BC=CD,
∴BCBE=CDDF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故③正确).
设EC=x,由勾股定理,得
EF=![]() x,CG=
x,CG=![]() x,
x,
AG=AEsin60=EFsin60=2×CGsin60=![]() x,
x,
∴AC=![]() ,
,
∴AB=![]() ,
,
∴BE=![]() x=
x=![]() ,
,
∴BE+DF=![]() xx≠
xx≠![]() x,(故④错误),
x,(故④错误),
∵S△CEF=![]() x2,
x2,
S△ABE= ![]() ,
,
∴2S△ABE=![]() x2=S△CEF,(故⑤正确).
x2=S△CEF,(故⑤正确).
综上所述,正确的有4个,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(3,1)在一次函数y=kx-2(k≠0)的图象上,则k的值是( )
A. 5 B. 4 C. 3 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB
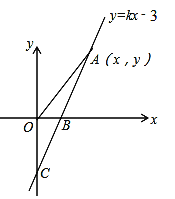
(1)求B点的坐标和k的值.
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当A 在运动的过程中,试写出△AOB的面积S与x的函数关系式,(不要求写出自变量的取值范围).
(3)探究:在(2)的条件下
①当A运动到什么位置时,△ABO的面积为
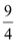 ,并说明理由.
,并说明理由.②在①成立的情况下,x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出满足条件的所有P点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
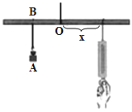
查看答案和解析>>【题目】如图所示,小华设计了一个研究杠杆平衡条件的实验,在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A,在中点的右侧用一个弹簧秤向下拉,改变弹簧与点O的距离x(cm)观察弹簧的示数y(N)的变化情况,实验数据记录如下:
(1)观察数据,求出y(N)与x(cm)之间的函数关系式,写出自变量的取值范围;

(2)当弹簧秤的示数是24N时,弹簧与点O的距离是多少?随着弹簧秤与点O的距离不断减小,弹簧秤上的示数将发生怎样的变化?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果﹣20%表示减少20%,那么+6%表示_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列不等式中成立的是( )
A. a+2<b+2 B. a﹣2<b﹣2 C. 2a<2b D. ﹣2a<﹣2b
相关试题

