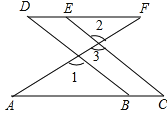
【题目】如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
参考答案:
【答案】因为∠l=∠2(已知)
∠2=∠3(对顶角相等)
所以∠l=∠3(等量代换)………………………………………………………2分
所以BD∥CE(同位角相等,两直线平行)……………………………………4分
所以∠C=∠DBA(两直线平行,同位角相等)………………………………6分
又因为∠C=∠D(已知)
所以∠DBA=∠D(等量代换)…………………………………………………8分
所以DF∥AC(内错角相等,两直线平行)………………………………………9分
所以∠A=∠F(两直线平行,内错角相等)…………………………………………10分
【解析】试题分析:根据对顶角的性质得到BD∥CE的条件,然后根据平行线的性质得到∠B=∠C,已知∠C=∠D,则得到满足AB∥EF的条件,再根据两直线平行,内错角相等得到∠A=∠F.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.
-
科目: 来源: 题型:
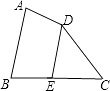
查看答案和解析>>【题目】如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
-
科目: 来源: 题型:
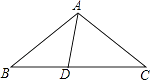
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:
(3)如图2:若BF、DG分别平分∠OBC、∠ODC的外角,判断BF与DG的位置关系,并说明理由。

-
科目: 来源: 题型:
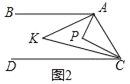
查看答案和解析>>【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
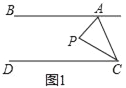
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
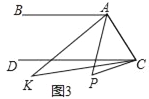
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于点D,∠B=∠DAC,点E在BC上,△EAC是以EC为底的等腰三角形,AB=4,AE=3.
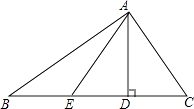
(1)判断△ABC的形状;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是 ( )
A. 经过路口,恰好遇到红灯; B. 四个人分成三组,这三组中有一组必有2人;
C. 打开电视,正在播放动画片; D. 抛一枚硬币,正面朝上;
相关试题

