【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;![]() ;
;![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;![]() ;
;![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
【解析】
逐一分析5条结论是否正确:(1)由抛物线与x轴有两个不相同的交点结合根的判别式即可得出该结论正确;(2)根据抛物线的对称轴为x=1,即可得出b=2a,即(2)正确;(3)根据抛物线的对称性找出点(![]() ,y3)在抛物线上,再结合抛物线对称轴左边的单调性即可得出(3)错误;(4)由x=3时,y<0,即可得出3a+c<0,结合b=2a即可得出(4)正确;(5)由方程at2+bt+a=0中△=b24aa=0结合a<0,即可得出抛物线y=at2+bt+a中y≤0,由此即可得出(5)正确.综上即可得出结论.
,y3)在抛物线上,再结合抛物线对称轴左边的单调性即可得出(3)错误;(4)由x=3时,y<0,即可得出3a+c<0,结合b=2a即可得出(4)正确;(5)由方程at2+bt+a=0中△=b24aa=0结合a<0,即可得出抛物线y=at2+bt+a中y≤0,由此即可得出(5)正确.综上即可得出结论.
(1)由函数图象可知,抛物线与x轴有两个不同的交点,
∴关于x的方程ax2+bx+c=0有两个不相等的实数根,
∴△=b24ac>0,
∴(1)正确;
(2)∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,
∴![]() =1,
=1,
∴2a=b,
∴(2)正确;
(3)∵抛物线的对称轴为x=1,点(![]() ,y3)在抛物线上,
,y3)在抛物线上,
∴(![]() ,y3).
,y3).
∵![]() <
<![]() <
<![]() ,且抛物线对称轴左边图象y值随x的增大而增大,
,且抛物线对称轴左边图象y值随x的增大而增大,
∴y1<y3<y2.
∴(3)错误;
(4)∵当x=3时,y=9a3b+c<0,且b=2a,
∴9a3×2a+c=3a+c<0,
∴6a+2c=3b+2c<0,
∴(4)正确;
(5)∵b=2a,
∴方程at2+bt+a=0中△=b24aa=0,
∴抛物线y=at2+bt+a与x轴只有一个交点,
∵图中抛物线开口向下,
∴a<0,
∴y=at2+bt+a≤0,
即at2+bt≤a=ab.
∴(5)正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,解决问题.
例题:若m2 +2mn+2n2-6n+9=0,求m和n的值.
解:∵ m2+2mn+2n2- 6n+9=0,
∴m2 +2mn+n2+n2-6n+9=0,
∴(m+n)2 +(n-3)2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
问题: (1)若2x2 +4x-2xy+y2 +4=0,求xy的值;
(2)已知a, b, c是△ABC的三边长,且满足a2+b2=10a+8b-41,求c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为弧
为弧 的中点,连接
的中点,连接 交
交 于点
于点 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 .
. 判断直线
判断直线 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;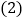 若
若 ,
,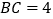 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°, 点D为射线CB上一点,且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上,截取AE=AD(点E与点C在直线AD的同侧),连接CE.
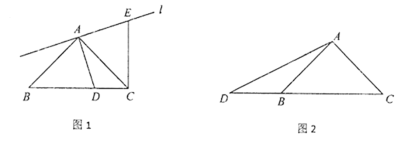
(1)当点D在线段CB上时,如图1,线段CE与BD的数量关系为____________,位置关系为___________;
(2)当点D在线段CB的延长线上时,如图2,
①请将图形补充完整;
②(1)中的结论是否仍成立?如果成立,请证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线
 图象的一部分,抛物线的顶点坐标
图象的一部分,抛物线的顶点坐标 ,与
,与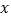 轴的一个交点
轴的一个交点 ,直线
,直线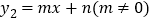 与抛物线交于
与抛物线交于 ,
, 两点,下列结论:
两点,下列结论:①
 ;②
;② ;③方程
;③方程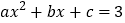 有两个相等的实数根;
有两个相等的实数根;④抛物线与
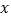 轴的另一个交点是
轴的另一个交点是 ;⑤当
;⑤当 时,有
时,有 ,
,其中正确的序号是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数
 的图象与
的图象与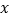 轴有两个交点,坐标分别为
轴有两个交点,坐标分别为 、
、 ,且
,且 ,图象上有一点
,图象上有一点 在
在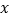 轴下方,在下列四个算式中判定正确的是________.
轴下方,在下列四个算式中判定正确的是________.①
 ;②
;② ;③
;③ ;④
;④ .
. -
科目: 来源: 题型:
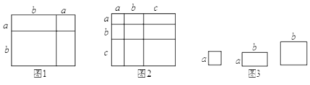
查看答案和解析>>【题目】(知识生成)我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2请解答下列问题:
(1)写出图2中所表示的数学等式________________;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a,b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=_______;
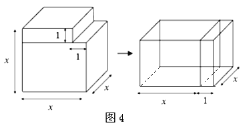
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个数学等式:_______________.
相关试题

